MoebiusMu[n]
gives the Möbius function ![]() .
.


MoebiusMu
MoebiusMu[n]
gives the Möbius function ![]() .
.
Details
- MoebiusMu is also known as Möbius function.
- Integer mathematical function, suitable for both symbolic and numerical manipulation.
- MoebiusMu[n] gives the sum of the primitive
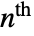 roots of unity.
roots of unity. - For a number n=u p1k1⋯ pmkm with u a unit and pi primes, MoebiusMu[n]returns 0 unless all ki are equal to 1, in which case it gives (-1)m.
- MoebiusMu[m+In] automatically works over Gaussian integers.
Examples
open all close allBasic Examples (2)
Scope (10)
Numerical Evaluation (4)
Symbolic Manipulation (6)
TraditionalForm formatting:
Use MoebiusMu in a sum:
Identify the MoebiusMu sequence:
Applications (11)
Basic Applications (2)
Highlight numbers n for which ![]() in blue, numbers n for which
in blue, numbers n for which ![]() in red and numbers n for which
in red and numbers n for which ![]() in black:
in black:
Histogram of the cumulative values of MoebiusMu:
Number Theory (9)
Use MoebiusMu to test for a square-free number:
Use MoebiusMu to compute the number of terms in the Farey sequence:
Use MoebiusMu to compute MangoldtLambda:
MoebiusMu is related to DivisorSigma through the Möbius inversion formulas:
MoebiusMu is related to PrimeNu through the following formula:
MoebiusMu satisfies the following identities:
Compute the number of polynomials over ![]() that are irreducible of degree n:
that are irreducible of degree n:
Irreducible polynomials modulo 5:
Distribution of irreducible polynomials modulo 5:
Logarithmic plot of the count for ![]() :
:
Plot the Mertens function ![]() [more info]:
[more info]:
Properties & Relations (7)
MoebiusMu is a multiplicative function:
![]() is 1 if n is a product of an even number of distinct primes:
is 1 if n is a product of an even number of distinct primes:
![]() is
is ![]() if it is a product of an odd number of primes:
if it is a product of an odd number of primes:
![]() is 0 if it has a multiple prime factor:
is 0 if it has a multiple prime factor:
MoebiusMu is 0 for composite prime powers and ![]() for primes:
for primes:
MoebiusMu is 0 for non-square-free integers:
Use PrimeNu to compute MoebiusMu for square-free numbers:
MoebiusMu is equal to the sum of the primitive ![]() roots of unity:
roots of unity:
MoebiusMu can be expressed in terms of LiouvilleLambda and KroneckerDelta:
See Also
Divisors SquareFreeQ FactorInteger DivisorSigma JacobiSymbol DivisorSum DirichletConvolve KroneckerDelta LiouvilleLambda PrimeOmega PrimeNu
Function Repository: RamanujanC
Tech Notes
Related Links
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), MoebiusMu, Wolfram Language function, https://reference.wolfram.com/language/ref/MoebiusMu.html.
CMS
Wolfram Language. 1988. "MoebiusMu." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MoebiusMu.html.
APA
Wolfram Language. (1988). MoebiusMu. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MoebiusMu.html
BibTeX
@misc{reference.wolfram_2025_moebiusmu, author="Wolfram Research", title="{MoebiusMu}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/MoebiusMu.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_moebiusmu, organization={Wolfram Research}, title={MoebiusMu}, year={1988}, url={https://reference.wolfram.com/language/ref/MoebiusMu.html}, note=[Accessed: 26-February-2026]}