JankoGroupJ4

JankoGroupJ4[]

散在型単純Janko群を表す．

詳細

JankoGroupJ4[]には置換表現は実装されていない．

予備知識

JankoGroupJ4[]は，位数がであるJanko群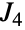を表す．この群は，位数が有限である26の散在型単純群の一つである．
Janko群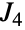は4番目に大きい散在型有限単純群である．この群は1970年代中頃に数学者のZvonimir Jankoによって発見された．この発見は散在型群の発見順で最後に位置する．JankoGroupJ4は，数多くの置換表現を持つ．その中でも最小のものは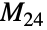，に関連する点固定群を有する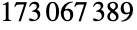のシンボルについてのもので，これは元が2つの体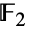上の特定の112次元の忠実表現として特定することもできる．Janko群は，他の散在型単純群とともに，有限単純群の重要（かつ完全）な分類に大きく貢献した．
JankoGroupJ4[]には，GroupOrder，GroupGenerators，GroupElements等を含む通常の群論関数を適用することができる．しかし，JankoGroupJ4[]は置換群ではあるが，位数が大きいために，明示的な置換表現の直接的な実装は非現実的である．結果として，そのような群論関数の数多くは適用されても未評価で返されることがある．Janko群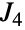の数多くの計算済みの特性を，FiniteGroupData[{"Janko",4},"prop"]を介して得ることができる．
JankoGroupJ4は他の数多くのシンボルに関連している．JankoGroupJ4は，モンスター群の部分商としては現れないために散在型有限単純群の「pariah」と呼ばれる6つの群の一つである（他にJankoGroupJ1，JankoGroupJ3，LyonsGroupLy，ONanGroupON，RudvalisGroupRuがあるがJankoGroupJ2は含まれない）．