Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ONanGroupON

represents the sporadic simple O'Nan group .

Details

No permutation representation is implemented for ONanGroupON[].

Background & Context

ONanGroupON[] represents the O'Nan group 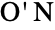, which is a group of order . It is one of the 26 sporadic simple groups of finite order and is sometimes known as the O'Nan–Sims group.
The O'Nan group is the thirteenth largest of the sporadic finite simple groups. It was discovered by mathematician Michael O'Nan and constructed explicitly by Charles Sims in the mid-1970s. ONanGroupON was first found while investigating groups having so-called Alperin-type Sylow 2-subgroups. The O'Nan group has a permutation representation on 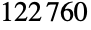symbols, a triple cover with a pair of 45-dimensional modular representations over field with seven elements, and a number of maximal subgroups, including the Janko group 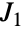, Mathieu group and the alternating group 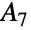. Along with the other sporadic simple groups, 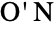played a foundational role in the monumental (and complete) classification of finite simple groups.
The usual group theoretic functions may be applied to ONanGroupON[], including GroupOrder, GroupGenerators, GroupElements and so on. However, while ONanGroupON[] is a permutation group, due its large order, an explicit permutation representation is impractical for direct implementation. As a result, a number of such group theoretic functions may return unevaluated when applied to it. A number of precomputed properties of the O'Nan group are available via FiniteGroupData["ONan","prop"].
ONanGroupON is related to a number of other symbols. Along with JankoGroupJ1, JankoGroupJ3, JankoGroupJ4, LyonsGroupLy and RudvalisGroupRu, ONanGroupON is one of six sporadic simple groups referred to as "pariahs" as a consequence of their failure to occur as subquotients of the monster group.

Examples

Basic Examples (1)

Order of the O'Nan group :

Top