RudvalisGroupRu

RudvalisGroupRu[]

represents the sporadic simple Rudvalis group .

Details

  • By default, RudvalisGroupRu[] is represented as a permutation group acting on points {1,…,4060}.

Background & Context

  • RudvalisGroupRu[] represents the Rudvalis group 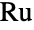, which is a group of order TemplateBox[{2, 14}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 3}, Superscript].7.13.29. It is one of the 26 sporadic simple groups of finite order. The default representation of RudvalisGroupRu is as a permutation group on the symbols 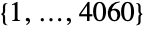having two generators.
  • The Rudvalis group 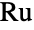is the twelfth smallest of the sporadic finite simple groups. It was discovered by mathematician Arunas Rudvalis and constructed explicitly by Conway and Wales in the early 1970s. RudvalisGroupRu was first defined in terms of a rank-3 action on 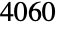symbols in which the stabilizer of a point is the so-called (non-simple) Ree group 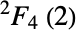of Lie type. The Rudvalis group has an automorphism group isomorphic to the Tits group, a double cover acting on a 28-dimensional lattice over the Gaussian integers, and a permutation representation that implies the existence of a strongly regular graph in which each vertex has 2304 neighbors (and 1755 non-neighbors) and any two adjacent vertices have 1328 common neighbors (as well as 1208 neighbors shared by nonadjacent ones). Along with the other sporadic simple groups, played a foundational role in the monumental (and complete) classification of finite simple groups.
  • The usual group theoretic functions may be applied to RudvalisGroupRu[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Rudvalis group are available via FiniteGroupData["Rudvalis","prop"].
  • RudvalisGroupRu is related to a number of other symbols. Along with JankoGroupJ1, JankoGroupJ3, JankoGroupJ4, LyonsGroupLy and ONanGroupON, RudvalisGroupRu is one of six sporadic simple groups referred to as "pariahs" as a consequence of their failure to occur as subquotients of the monster group.

Examples

Basic Examples  (3)

Order of the Rudvalis group:

Number of points moved by the generators of a permutation representation of the Rudvalis group:

Order of a pseudorandom element of the Rudvalis group:

Wolfram Research (2010), RudvalisGroupRu, Wolfram Language function, https://reference.wolfram.com/language/ref/RudvalisGroupRu.html.

Text

Wolfram Research (2010), RudvalisGroupRu, Wolfram Language function, https://reference.wolfram.com/language/ref/RudvalisGroupRu.html.

CMS

Wolfram Language. 2010. "RudvalisGroupRu." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RudvalisGroupRu.html.

APA

Wolfram Language. (2010). RudvalisGroupRu. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RudvalisGroupRu.html

BibTeX

@misc{reference.wolfram_2024_rudvalisgroupru, author="Wolfram Research", title="{RudvalisGroupRu}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/RudvalisGroupRu.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rudvalisgroupru, organization={Wolfram Research}, title={RudvalisGroupRu}, year={2010}, url={https://reference.wolfram.com/language/ref/RudvalisGroupRu.html}, note=[Accessed: 22-December-2024 ]}