グラフ g のKirchhoff行列を返す.
KirchhoffMatrix[{vw,…}]
規則 vw を使ってグラフ g を指定する.


KirchhoffMatrix
グラフ g のKirchhoff行列を返す.
KirchhoffMatrix[{vw,…}]
規則 vw を使ってグラフ g を指定する.
詳細

- KirchhoffMatrixはラプラシアン(Laplacian)行列としても知られている.
- KirchhoffMatrixはSparseArrayオブジェクトを返す.これはNormalを使って通常の行列に変換できる.
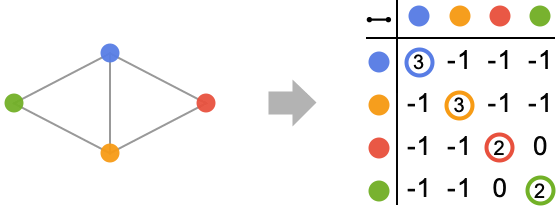
- 対角項 ki,iは viの次数に等しい.
- 頂点 viが vjと連結されている場合,項 ki,jは-1である.
- 頂点 viはVertexList[g]で返されるものと同じ順序であると想定される.
- グラフのKirchhoff行列の次元は
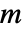 ×
×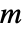 である.ただし,
である.ただし,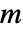 は頂点の数である.
は頂点の数である.
予備知識
- KirchhoffMatrixは,ラプラシアン(Laplacian)行列,アドミタンス行列,あるいは離散ラプラシアンとしても知られる,Kirchhoff行列を返す.これは,整数要素の正方行列である.効率のため,KirchhoffMatrixは行列を疎な配列として返す.(通常の)Kirchhoff行列 L は,次数行列 D (グラフの頂点次数
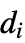 の対角行列)と隣接行列 A の差 L=D-A として定義され,L の対角要素
の対角行列)と隣接行列 A の差 L=D-A として定義され,L の対角要素 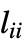 は,したがって,頂点
は,したがって,頂点 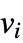 の次数
の次数 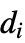 に等しく,非対角要素
に等しく,非対角要素 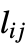 は,頂点
は,頂点 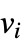 が
が 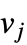 に隣接している場合は
に隣接している場合は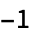 で,その他の場合は0である.
で,その他の場合は0である. - n 個の頂点があるグラフの場合,Kirchhoff行列の次元は n×n である.無向グラフの場合,Kirchhoff行列は対称である.
- Kirchhoff行列は,スペクトルグラフ理論の中心的役割を果たす.この理論は,隣接行列あるいはKirchhoff行列の固有値に基づいてグラフを研究するものである.これを使って,グラフの頂点間の抵抗距離を計算することができる.これは,各辺が単位抵抗で置換された場合の(電池が頂点に付属している)頂点間の実効抵抗として定義することができる.これは,行列木定理にも見られる.この定理は,グラフの全域木の数を与えるものである.Kirchhoff行列の2番目に小さい固有値はグラフの代数連結性として知られており,グラフはこの固有値が0より大きいときかつそのときに限り連結されている.グラフの代数連結性に対応する固有値はFiedlerベクトルとして知られており,隣接行列あるいはKirchhoff行列の固有値に基づいて指定されたグラフを特定の特性を持つより小さい成分に分割するスペクトルグラフ分割において重要である
- 物理学者は「Kirchhoff行列」の代りに「ラプラシアン行列」という語を好んで使うのに注意のこと.物理学者や数学者の中には,i=j かつ
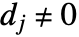 のときは
のときは 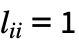 ,
,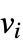 と
と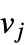 が隣接しているなら
が隣接しているなら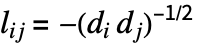 ,その他の場合は0という,正規化が異なるバージョンも使う.さらに,「グラフスペクトル」という語は,一般に,数学者にとってはグラフの隣接行列の固有値を意味するのに対し,物理学者にとっては,これはしばしば正規化されたKirchhoff行列の固有値を意味する.であるから,これらの語が孤立して出てきた場合は注意が必要である.
,その他の場合は0という,正規化が異なるバージョンも使う.さらに,「グラフスペクトル」という語は,一般に,数学者にとってはグラフの隣接行列の固有値を意味するのに対し,物理学者にとっては,これはしばしば正規化されたKirchhoff行列の固有値を意味する.であるから,これらの語が孤立して出てきた場合は注意が必要である. - KirchhoffGraphを使ってKirchhoff行列からグラフを構成することができる.類似した関数のAdjacencyGraphおよびIncidenceGraphは,与えられた隣接行列および結合行列からグラフを構築する.
例題
すべて開く すべて閉じるスコープ (5)
特性と関係 (8)
Kirchhoff行列の行と列はVertexListで与えられる順に従う:
KirchhoffGraphを使ってKirchhoff行列からグラフを構築する:
頂点の次数はKirchhoff行列の対角を使って求めることができる:
完全グラフの場合,対角外の項はすべてKirchhoff行列では![]() である:
である:
特に,TuranGraphとStarGraphは二部グラフである:
関連項目
KirchhoffGraph AdjacencyMatrix IncidenceMatrix WeightedAdjacencyMatrix VertexIndex
Function Repository: KirchhoffTensor
関連するガイド
-
▪
- グラフと行列 ▪
- グラフの構築と表現 ▪
- グラフプログラミング
テキスト
Wolfram Research (2010), KirchhoffMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/KirchhoffMatrix.html (2015年に更新).
CMS
Wolfram Language. 2010. "KirchhoffMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/KirchhoffMatrix.html.
APA
Wolfram Language. (2010). KirchhoffMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KirchhoffMatrix.html
BibTeX
@misc{reference.wolfram_2025_kirchhoffmatrix, author="Wolfram Research", title="{KirchhoffMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_kirchhoffmatrix, organization={Wolfram Research}, title={KirchhoffMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}, note=[Accessed: 06-February-2026]}