给出图 g 的基尔霍夫矩阵.
KirchhoffMatrix[{vw,…}]
使用规则 vw 指定图 g.


KirchhoffMatrix
给出图 g 的基尔霍夫矩阵.
KirchhoffMatrix[{vw,…}]
使用规则 vw 指定图 g.
更多信息

- KirchhoffMatrix 也称为拉普拉斯矩阵.
- KirchhoffMatrix 返回一个 SparseArray 对象,该对象可以用 Normal 转化为一个普通矩阵.
- 对角线元素 ki,i 等于 vi 的度数.
- 元素 ki,j 等于 -1,如果顶点 vi 与 vj 相邻接.
- 假设顶点 vi 遵循由 VertexList[g] 给出的顺序.
- 一个图的基尔霍夫矩阵具有维度
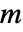 ×
×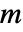 ,其中
,其中 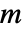 是顶点数.
是顶点数.
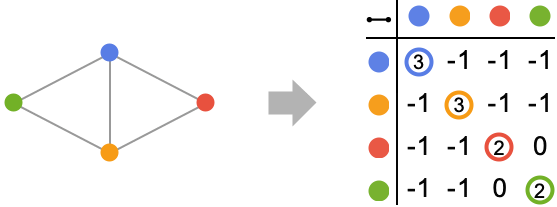
背景
- KirchhoffMatrix 返回基尔霍夫矩阵,也被称为拉普拉斯矩阵、导纳矩阵、或离散拉普拉斯算子. 这是一个以整数为元素的方阵. 出于效率,KirchhoffMatrix 返回的是稀疏数组. (通常)基尔霍夫矩阵 L 被定义为度数矩阵 D (图顶点度数
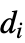 的对角矩阵)和邻接矩阵 A 之差 L=D-A. 因此 L 的对角元素
的对角矩阵)和邻接矩阵 A 之差 L=D-A. 因此 L 的对角元素 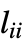 等于顶点
等于顶点 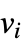 的度数
的度数 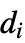 而不在对角线上的元素
而不在对角线上的元素 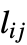 等于
等于 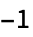 若顶点
若顶点 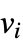 与
与 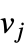 相邻,否则为 0.
相邻,否则为 0. - 对有 n 个顶点的图,基尔霍夫矩阵大小为 n×n. 对无向图,基尔霍夫矩阵是对称的.
- 基尔霍夫矩阵在谱图理论中起着核心的作用,谱图理论是基于图邻接矩阵或基尔霍夫矩阵的特征值的对图的研究. 它可被用于计算图中顶点之间的电阻距离,后者被定义为把每条图的边都替换为单位电阻后,顶点之间有效电阻的大小(当有电池与他们连在一起时). 它还出现在了矩阵树定理中,这一定理给出了图的生成树的数量. 基尔霍夫矩阵的第二最小特征值被称为图的代数连通度,一个图是连通的当且仅当该特征值大于 0. 图的代数连通度对应的特征向量被称为 Fiedler 向量并在谱图分割十分重要. 谱图分割是一种根据某种性质而把图分割成较小部分的一种分割,这个性质基于邻接矩阵或基尔霍夫矩阵的特征值.
- 注意到物理学家通常使用术语“拉普拉斯矩阵”而不是“基尔霍夫矩阵”. 一些物理学家和数学家还使用一种不同的规范化的矩阵版本,即定义为令
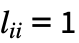 若 i=j 且
若 i=j 且 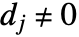 ,
,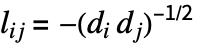 若
若 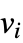 和
和 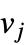 相邻,否则为 0. 此外,尽管对数学家而言术语“图谱”一般指的是图邻接矩阵的特征值,但对物理学家而言它常常指的是规范化基尔霍夫矩阵的特征值. 因此一般情况下遇到这些术语时需要特别小心.
相邻,否则为 0. 此外,尽管对数学家而言术语“图谱”一般指的是图邻接矩阵的特征值,但对物理学家而言它常常指的是规范化基尔霍夫矩阵的特征值. 因此一般情况下遇到这些术语时需要特别小心. - KirchhoffGraph 可被用于从基尔霍夫矩阵构造图. 有类似的函数 AdjacencyGraph 和 IncidenceGraph 分别从邻接矩阵和关联矩阵来构造图.
范例
打开所有单元 关闭所有单元范围 (5)
KirchhoffMatrix 对大规模图起作用:
使用 MatrixPlot 来对矩阵进行可视化处理:
属性和关系 (8)
基尔霍夫矩阵的行和列遵循由 VertexList 给出的顺序:
使用 KirchhoffMatrix 来从一个基尔霍夫矩阵中构建一个图:
特别地,TuranGraph 和 StarGraph 是二部图:
参见
KirchhoffGraph AdjacencyMatrix IncidenceMatrix WeightedAdjacencyMatrix VertexIndex
Function Repository: KirchhoffTensor
文本
Wolfram Research (2010),KirchhoffMatrix,Wolfram 语言函数,https://reference.wolfram.com/language/ref/KirchhoffMatrix.html (更新于 2015 年).
CMS
Wolfram 语言. 2010. "KirchhoffMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/KirchhoffMatrix.html.
APA
Wolfram 语言. (2010). KirchhoffMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KirchhoffMatrix.html 年
BibTeX
@misc{reference.wolfram_2025_kirchhoffmatrix, author="Wolfram Research", title="{KirchhoffMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_kirchhoffmatrix, organization={Wolfram Research}, title={KirchhoffMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/KirchhoffMatrix.html}, note=[Accessed: 10-March-2026]}