KroneckerModelDecomposition

KroneckerModelDecomposition[ssm]

yields the Kronecker decomposition of a descriptor state-space model ssm.

Details and Options

  • The Kronecker decomposition is also known as the Weierstrass decomposition.
  • The result is a list {{p,q},kssm}, where p and q are transformation matrices, and kssm is the Kronecker form of ssm.
  • The decomposition decouples a descriptor state-space model into slow and fast subsystems.
  • The slow subsystem has the same form as a standard state-space model with state equation:
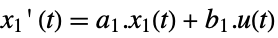
  • continuous time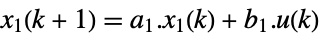
    discrete time
  • The fast subsystem is governed by the following state equations where e2 is nilpotent:
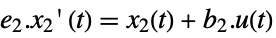
  • continuous time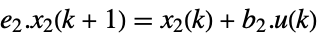
    discrete time
  • The output of the system in Kronecker form is:
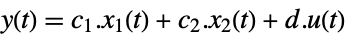
  • continuous time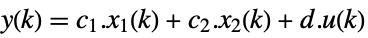
    discrete time
  • The matrices a1 and e2 are both taken to be in Jordan form.
  • StateSpaceTransform[ssm,{p,q}] has the form StateSpaceModel[{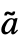,,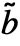,,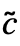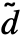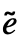}], with 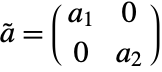and 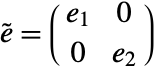, where 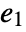and a2 are identity matrices with the dimensions of the slow and fast subsystems, and 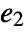is a nilpotent matrix.

Examples

open allclose all

Basic Examples  (1)

Compute the Kronecker decomposition of a state-space model:

Scope  (4)

The Kronecker decomposition of a system with two fast states and two slow states:

The Kronecker decomposition of a discrete-time system:

An algebraic system:

An impulsive system:

Applications  (2)

KroneckerModelDecomposition decouples the fast and slow subsystems:

The number of 1s on the diagonal of the descriptor matrix gives the number of slow states:

Separate the slow and fast systems using SystemsModelExtract and SystemsModelDelete:

An RLC circuit modeled as a descriptor state space:

Properties & Relations  (6)

The Kronecker decomposition and the original system are restricted equivalent systems:

They have the same order:

They have the same controllability and observability properties:

They have the same transfer functions:

Nonsingular systems give an identity matrix for the descriptor matrix:

Find the Kronecker decomposition of a singular descriptor state-space model:

The matrix pair {p,q} relates the original system to the Kronecker form:

The inverse matrices perform the opposite transformation:

The slow and fast subsystems model the proper and improper parts of a transfer function:

The state matrix in the slow subsystem is in Jordan form:

The descriptor matrix in the fast subsystem is in Jordan form with all zero eigenvalues:

Wolfram Research (2012), KroneckerModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html.

Text

Wolfram Research (2012), KroneckerModelDecomposition, Wolfram Language function, https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html.

CMS

Wolfram Language. 2012. "KroneckerModelDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html.

APA

Wolfram Language. (2012). KroneckerModelDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html

BibTeX

@misc{reference.wolfram_2024_kroneckermodeldecomposition, author="Wolfram Research", title="{KroneckerModelDecomposition}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_kroneckermodeldecomposition, organization={Wolfram Research}, title={KroneckerModelDecomposition}, year={2012}, url={https://reference.wolfram.com/language/ref/KroneckerModelDecomposition.html}, note=[Accessed: 22-November-2024 ]}