WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

KroneckerModelDecomposition

KroneckerModelDecomposition[ssm]

ディスクリプタ状態空間モデル ssm のクロネッカー(Kronecker)分解を与える．

詳細とオプション

クロネッカー分解はワイエルシュトラス(Weierstrass)分解としても知られている．
結果はリスト{{p,q},kssm}である．ただし，p および q は変換行列であり，kssm は ssm のクロネッカー形である．
分解はディスクリプタ状態空間モデルを高速部分系と低速部分系に分離する．
低速部分系は，状態方程式がある標準状態空間モデルと同じ形式である．
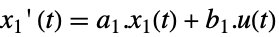
連続時間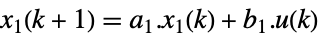

離散時間
高速部分系は次の e₂がベキ零である状態方程式で支配されている．
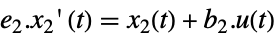
連続時間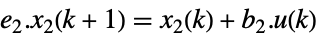

離散時間
クロネッカー形式の系の出力
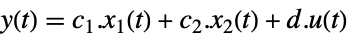
連続時間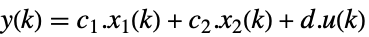

離散時間
行列 a₁および e₂は両方ともジョルダン(Jordan)形式であると解釈される．
StateSpaceTransform[ssm,{p,q}]の形式は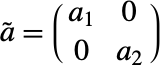および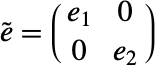を持つStateSpaceModel[{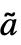,,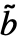,,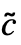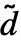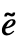}]である．ただし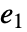，および a₂は次元が低速および高速の部分系の恒等行列であり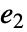，はベキ零行列である．

例題

すべて開くすべて閉じる

例 (1)

状態空間モデルのクロネッカー分解を計算する：

スコープ (4)

2つの速い状態と2つの遅い状態がある系のクロネッカー分解：

離散時間系のクロネッカー分解：

代数系：

インパルス系：

アプリケーション (2)

KroneckerModelDecompositionは速い部分系と遅い部分系を分離する：

ディスクリプタ行列の対角上にある1の数は遅い状態の数を与える：

SystemsModelExtractおよびSystemsModelDeleteを使って遅い系と速い系を分離する：

ディスクリプタ状態空間としてモデル化されたRLC回路：

特性と関係 (6)

クロネッカー分解ともとの系は制約のある等価系である：

両者の次数は等しい：

どちらも同じ可制御性と可観測性の特性を持つ：

どちらも同じ伝達関数を持つ：

非特異系はディスクリプタ行列に対して恒等行列を与える：

特異ディスクリプタ状態空間モデルのクロネッカー分解を求める：

行列のペア{p,q}はもとの系とクロネッカー形式を関連付ける：

逆行列は逆の変換を行う：

遅い部分系と速い部分系で伝達関数の適切な部分と適切ではない部分をモデル化する：

遅い部分系の状態行列はジョルダン形である：

速い部分系のディスクリプタ行列はすべての零固有値を含むジョルダン形である：

トップへ