Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

LameCPrime

LameCPrime

LameCPrime[ν,j,z,m]

gives the -derivative of the Lamé function of order with elliptic parameter .

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
LameCPrime belongs to the Lamé class of functions.
For certain special arguments, LameCPrime automatically evaluates to exact values.
LameCPrime can be evaluated to arbitrary numerical precision for an arbitrary complex argument.
LameCPrime automatically threads over lists.
LameCPrime[ν,0,z,0]=0 and LameCPrime[ν,j,z,0]=j Sin[j(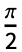-z)].

Examples

open all close all

Basic Examples (3)

Evaluate numerically:

Plot the LameCPrime function for and :

Series expansion of LameCPrime at the origin:

Scope (26)

Numerical Evaluation (5)

Evaluate to high precision:

The precision of the output tracks the precision of the input:

LameCPrime can take complex number parameters and argument:

Evaluate LameCPrime efficiently at high precision:

Lists and matrices:

Specific Values (3)

Value of LameCPrime when and :

Value of LameCPrime when and :

Some poles of LameCPrime:

For integer values of and , LameCPrime can be expressed entirely in terms of Jacobi elliptic functions:

Visualization (6)

Plot the first three even LameCPrime functions:

Plot the first three odd LameCPrime functions:

Plot the absolute value of the LameCPrime function for complex parameters:

Plot LameCPrime as a function of its first parameter :

Plot LameCPrime as a function of and elliptic parameter :

Plot the family of LameCPrime functions for different values of the elliptic parameter :

Function Properties (2)

When is even, LameCPrime is a periodic function of real argument with a period 2EllipticK[m] and has an initial value LameCPrime[ν,j,0,m]=0:

When is odd, LameCPrime is a periodic function of real argument with a period 4EllipticK[m]:

Differentiation (2)

The -derivative of LameCPrime involves LameC function:

Derivatives of LameCPrime for specific cases of parameters:

Integration (3)

Indefinite integral of LameCPrime is LameC:

Definite numerical integrals of LameCPrime:

More integrals with LameCPrime:

Series Expansions (3)

Series expansion of LameCPrime at the origin:

Coefficient of the second term of this expansion:

Plot the first- and third-order approximations for LameCPrime around :

Series expansion for LameCPrime at any ordinary complex point:

Function Representations (2)

LameCPrime cannot be represented in terms of MeijerG:

TraditionalForm formatting:

Applications (1)

Use the LameCPrime function to calculate the derivatives of LameC:

Properties & Relations (2)

LameCPrime is an even function when is a positive odd integer:

LameCPrime is an odd function when is a non-negative even integer:

Use FunctionExpand to expand LameCPrime for integer values of and :

Possible Issues (1)

LameCPrime is not defined if is a negative integer:

LameCPrime is not defined if is not an integer:

Top