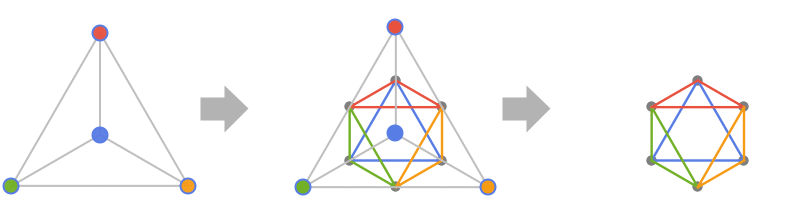
LineGraph
背景
- LineGraph 返回
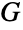 的线图
的线图 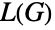 ,其顶点是
,其顶点是 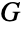 的边而其顶点邻接对应于
的边而其顶点邻接对应于 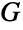 的边邻接. 更正式地,给定有边 e1,…,em 的图
的边邻接. 更正式地,给定有边 e1,…,em 的图 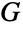 ,则其
,则其 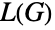 有顶点 e1,…,em. 对于无向图
有顶点 e1,…,em. 对于无向图 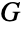 ,若
,若 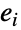 和
和 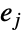 入射于
入射于 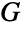 中的相同顶点则
中的相同顶点则  是
是 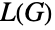 中的边,而对于有向图
中的边,而对于有向图 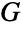 ,若图
,若图 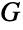 中
中 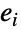 的头部是
的头部是 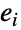 的尾部则
的尾部则  是
是 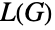 中的边. 线图也称作伴随图、共轭图、覆盖图、衍生图、导出图、边图、边-点对偶图、代表图或
中的边. 线图也称作伴随图、共轭图、覆盖图、衍生图、导出图、边图、边-点对偶图、代表图或 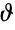 -obrazom 图.
-obrazom 图. - 线图被用于将图的关于顶点的理论结果翻译成关于边的结果. 例如,
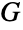 中的独立边集是
中的独立边集是 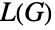 中的独立顶点集,
中的独立顶点集, 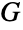 的边色数等于
的边色数等于 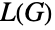 的色数等等.
的色数等等. - 线图通过一系列数学关系与其原始图相连接. 其中最简单的关系即
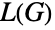 的顶点数目等于
的顶点数目等于 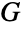 的边数目. 另外,如果
的边数目. 另外,如果 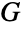 是一个有
是一个有 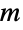 条边和点指数为 d1,…,dn 的
条边和点指数为 d1,…,dn 的 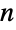 个顶点的简单图,则
个顶点的简单图,则 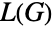 中的边数目为
中的边数目为 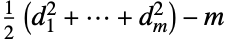 . 另一个允许线图显式结构的关系是对于简单图
. 另一个允许线图显式结构的关系是对于简单图 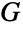 的关联矩阵
的关联矩阵 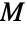 和 m×m 的单位矩阵
和 m×m 的单位矩阵 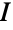 ,
, 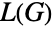 的相邻矩阵由
的相邻矩阵由 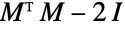 给出.
给出. - 一个图是否为线图的判定可以在线性时间内做出. 当且仅当存在一个团族,图
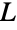 中的各顶点正好含有其中的两个元素,并且图
中的各顶点正好含有其中的两个元素,并且图 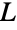 中的各边由其中的一个元素引发时,图
中的各边由其中的一个元素引发时,图 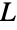 是简单图或多重图的线图. 若这个团族中
是简单图或多重图的线图. 若这个团族中 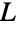 的任意两个顶点不再两个相同的团中,则
的任意两个顶点不再两个相同的团中,则 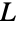 是简单图的线图.
是简单图的线图. - 若有含有九个禁向图的集合,各图至多有六个顶点,那么当且仅当其中不含作为该集合中诱导子图的图时,简单图是某些简单图的线图. 这个禁向图的集合由 GraphData["Beineke"] 给出并包含完整二分图
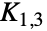 ,所以线图是无爪图. 这些禁向图中只有六个需要显示哪个有不少于5的最大度的简单图是线图(参见 GraphData["Metelsky"]).
,所以线图是无爪图. 这些禁向图中只有六个需要显示哪个有不少于5的最大度的简单图是线图(参见 GraphData["Metelsky"]). - 图论中的许多重要结果描述线图的特性. 例如,Vizing 理论意味着如果
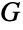 是个不含三角的简单图,则
是个不含三角的简单图,则 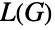 的色数等于
的色数等于 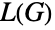 中最大团的大小或比起多一,而 König 线着色理论一表明一个两偶图的线图
中最大团的大小或比起多一,而 König 线着色理论一表明一个两偶图的线图 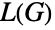 是完美的(即
是完美的(即 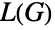 的各诱导子图的色数等于该子图的最大团的大小).
的各诱导子图的色数等于该子图的最大团的大小).
范例
打开所有单元关闭所有单元
Wolfram Research (2010),LineGraph,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LineGraph.html (更新于 2015 年).
文本
Wolfram Research (2010),LineGraph,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LineGraph.html (更新于 2015 年).
CMS
Wolfram 语言. 2010. "LineGraph." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/LineGraph.html.
APA
Wolfram 语言. (2010). LineGraph. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LineGraph.html 年