LogLikelihood
LogLikelihood[dist,{x1,x2,…}]
给出来自分布 dist 的观察值 x1、x2、… 的对数似然值.
LogLikelihood[proc,{{t1,x1},{t2,x2},…}]
给出来自过程 proc 的时间 ti 的观测值 xi 的对数似然函数.
LogLikelihood[proc,{path1,path2,…}]
给出来自过程 proc 的 path1、path2、… 的观测值的对数似然函数.
更多信息

- 对数似然值 LogLikelihood[dist,{x1,x2,…}] 由
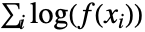 给出,其中
给出,其中 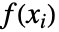 是位于 xi 的概率密度值,PDF[dist,xi].
是位于 xi 的概率密度值,PDF[dist,xi]. - 对于标量值过程 proc,对数似然值函数 LogLikelihood[proc,{{t1,x1},{t2,x2},…}] 由 LogLikelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,x2,…}}] 给出.
- 对于向量值过程 proc,对数似然值函数 LogLikelihood[proc,{{t1,{x1,…,z1},{t2,{x2,…,z2}},…}] 由 LogLikelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,…,z1,x2,…,z2,…}}] 给出.
- 路径集合的对数似然值 LogLikelihood[proc,{path1,path2,…}] 由
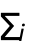 LogLikelihood[proc,pathi] 给出.
LogLikelihood[proc,pathi] 给出.
范例
打开所有单元关闭所有单元范围 (12)
导出分布 (5)
应用 (4)
属性和关系 (5)
LogLikelihood 是数据的 PDF 值的对数的和:
LogLikelihood 是 Likelihood 的对数:
EstimatedDistribution 通过最大化对数似然值估计参数:
FindDistributionParameters 把参数估计作为规则给出:
将路径值向量化,以用于时间切片分布的 LogLikelihood:
给定一个分布 的样本, 的 LogLikelihood 的值和 MLE 估计所得分布之间的差的两倍是随机的,且服从 ChiSquareDistribution,自由度等于分布参数的个数:
文本
Wolfram Research (2010),LogLikelihood,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LogLikelihood.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "LogLikelihood." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/LogLikelihood.html.
APA
Wolfram 语言. (2010). LogLikelihood. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LogLikelihood.html 年