LogRankTest

LogRankTest[{data1,data2,…}]

対数順位型の検定を使って datai中のハザード率の等価性の検定を行う．

LogRankTest[{data1,data2,…},wspec]

重み wspec の加重対数順位検定を行う．

LogRankTest[{data1,…},wspec,"property"]

"property"の値を返す．

詳細とオプション

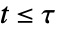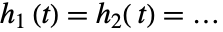  • LogRankTestは，dataiに対して，母集団の真のハザード率がすべての について に等しいという帰無仮説 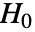と，少なくとも1つの 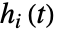が 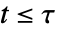の何らかの値について異なっているという対立仮説 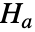で仮説検定を行う．
  • 数 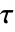は一般に dataiにおける最大の事象時間であると考えられる．
  • デフォルトで，確率値つまり 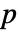値が返される．
  • 小さい 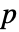値は 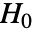が真である可能性が低いことを示す．
  • datai は一変量{x1,x2,…}でなければならない．
  • dataiはSparseArrayあるいはEventDataオブジェクトでよい．
  • LogRankTestは事実上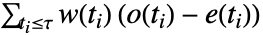に基づいている．ただし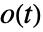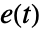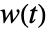，，，は順に，事象の観察数，合併サンプルに基づく事象の期待値，何らかの重みを表す．
  • 名前付きの加重メソッドの場合，時間 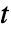における重み 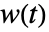は，一般に，リスクにさらされている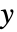数 ，事象数 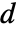，プールされているサンプル中の積極限推定量 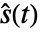あるいはプールされているサンプルの同様の推定量 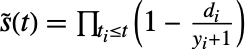に基づく．
  • 次の重み指定 wspec を使うことができる．
  • ρ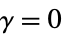のFleming–Harrington重み
    {ρ,γ}完全に指定されたFleming–Harrington重み
    "name"名前付き加重メソッドを使う
  • ρ と γ の値は非負の数でよい．
  • ρ と γ を指定すると 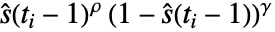の形式のFleming–Harrington重みが与えられる．
  • 使用可能な名前付きの重み指定
  • "AndersenPeto"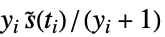y_(i)s^~(t_(i))/(y_(i)+1)
    "Equal"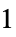
    "Gehan"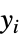
    "Peto"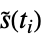
    "TaroneWare"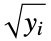
  • 区間打切りデータについてはZhao–Zhao–Sun–Kimの一般化された対数順位検定が使われる．
  • LogRankTest[{data1,…},wspec,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．このオブジェクトは，htd["property"] の形を使った追加的な検定結果と特性の抽出に使うことができる．
  • LogRankTest[{data1,…},wspec,"property"]を使って"property"の値を直接与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定に使われる自由度
    "EventTimes"検定に使われる時間点のリスト
    "EventWeights"各事象時間で使われる重みのリスト
    "PValue" 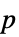値のリスト
    "PValueTable" 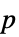値のフォーマットされた表
    "ShortTestConclusion"検定結果の短い記述
    "TestConclusion"検定結果の記述
    "TestData"検定統計量と 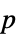値のペアのリスト
    "TestDataTable" 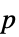値と検定統計量のフォーマットされた表
    "TestStatistic"検定統計量のリスト
    "TestStatisticTable"検定統計量のフォーマットされた表
  • 使用可能なオプション
  • Method Automatic 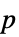値の計算に使うメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て

例題

すべて開くすべて閉じる

例  (4)

サンプルデータを使ってハザード率を比較する：

繰り返して特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

打切りデータの検定を行う：

5%水準で有意差が検出された：

加重対数順位検定を行う：

名前付きの加重スキームを使う：

Fleming–Harringtonの重みを使う：

多くのサンプルで等しいハザード率について検定を行う：

生存率を視覚的に比較する：

有意差は検出されない：

スコープ  (11)

検定  (7)

対数順位検定から 値を得る：

多くの群の検定を同時に行う：

加重対数順位検定についての 値を計算する：

名前付きの加重スキーム：

Fleming–Harringtonタイプの重みを手動で設定する：

で のFleming–Harringtonの重み：

完全に指定されたFleming–Harringtonタイプの重みを使う：

で のFleming–Harringtonの重み：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

値と検定統計量：

任意数の特性を同時に抽出する：

値，検定統計量，それに自由度：

レポート  (4)

検定結果を表にする：

表からの値：

カスタムレポートのために特性を取り出す：

値と検定統計量を表にする：

検定に使われた正規化された重みを可視化する：

名前付きの加重スキームは初期事象を強調する傾向がある：

Fleming–Harringtonの重みを使って他の事象領域を強調することができる：

オプション  (4)

Method  (3)

デフォルトで，検定統計量の漸近的 分布を使って 値が計算される：

ランダムな置換に基づいた検定の方が少ないサンプル数でよい結果を与えることがある：

実行するランダム置換の回数を指定する：

250回のランダム置換を指定する：

ランダム置換の生成に使用したシードを改める：

シード9を使う：

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に使われる：

特性と関係  (7)

デフォルトで，検定統計量は の下でChiSquareDistributionに従うと仮定される：

加重スキームによって時間上の特定の点を強調することができる：

名前付きのスキームは初期事象により重きを置く傾向がある：

Fleming–Harrington母数を使うと加重を細かく制御することができる：

MannWhitneyTestを打切りのない2つのサンプルに使うことができる：

検定は漸近的に等しい：

Kruskal–Wallis検定を打切りのない3つ以上のサンプルに使うことができる：

検定は漸近的に等しい：

SurvivalModelFitを使って生存確率を推定することができる：

生存曲線を推定する：

生存確率が30での95%信頼区間を作る：

CoxModelFitを使って共分散がある場合の生存確率を推定する：

母数推定を得る：

共分散水準の かつ での生存推定を可視化する：

対数順位検定は，TemporalDataの経路構造を認識する：

値を直接使う：

Wolfram Research (2012), LogRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/LogRankTest.html.

テキスト

Wolfram Research (2012), LogRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/LogRankTest.html.

CMS

Wolfram Language. 2012. "LogRankTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogRankTest.html.

APA

Wolfram Language. (2012). LogRankTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogRankTest.html

BibTeX

@misc{reference.wolfram_2024_logranktest, author="Wolfram Research", title="{LogRankTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/LogRankTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_logranktest, organization={Wolfram Research}, title={LogRankTest}, year={2012}, url={https://reference.wolfram.com/language/ref/LogRankTest.html}, note=[Accessed: 22-November-2024 ]}