LowerTriangularMatrix

LowerTriangularMatrix[lmat]

converts the lower triangular matrix lmat to a structured array.

Details and Options

  • Lower triangular matrices, when represented as structured arrays, allow for efficient storage and more efficient operations, including Det, Inverse and LinearSolve.
  • Lower triangular matrices occur when solving linear systems of equations, where they represent simple systems that can be solved by forward substitution. Matrix decompositions that use lower and upper triangular matrices include LU, LDL, LL (Cholesky) and LQ decompositions.
  • A lower triangular matrix 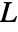satisfies 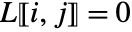for .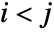
  • The elements lij need not be numerical.
  • The inverse of a lower triangular matrix is another lower triangular matrix.
  • Lower triangular matrices are closed under matrix multiplication, so 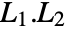is again a lower triangular matrix.
  • The determinant of a lower triangular matrix is given by the product of the diagonal elements .
  • Operations that are accelerated for LowerTriangularMatrix include:
  • Dettime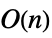
    Dottime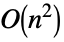
    LinearSolvetime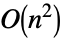
  • For a LowerTriangularMatrix sa, the following properties "prop" can be accessed as sa["prop"]:
  • "Matrix"lower triangular matrix, represented as a full array
    "Properties"list of supported properties
    "Structure"type of structured array
    "StructuredData"internal data stored by the structured array
    "StructuredAlgorithms"list of functions with special methods for the structured array
    "Summary"summary information, represented as a Dataset
  • Normal[LowerTriangularMatrix[…]] gives the lower triangular matrix as an ordinary matrix.
  • LowerTriangularMatrix[…,TargetStructure->struct] returns the lower triangular matrix in the format specified by struct. Possible settings include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Sparse"represent the matrix as a sparse array
    "Structured"represent the matrix as a structured array
  • LowerTriangularMatrix[…,TargetStructureAutomatic] is equivalent to LowerTriangularMatrix[…,TargetStructure"Structured"].

Examples

open allclose all

Basic Examples  (2)

Construct a lower triangular matrix:

Show the elements:

Normal can convert a LowerTriangularMatrix to its ordinary representation:

Construct a lower triangular matrix with symbolic entries:

Show the elements:

Get the determinant:

Scope  (5)

LowerTriangularMatrix objects include properties that give information about the matrix:

The "Summary" property gives a brief summary of information about the matrix:

The "StructuredAlgorithms" property lists the functions that have structured algorithms:

Structured algorithms are typically faster:

Compute the determinant:

Compute the inverse:

Solve a linear system:

Compute the eigenvalues:

When appropriate, structured algorithms return another LowerTriangularMatrix object:

Inverting lt gives another lower triangular matrix:

Transposing lt gives an upper triangular matrix:

The product of lt with its transpose is no longer a triangular matrix:

Construct a lower triangular matrix from a SparseArray with integer entries:

Show the elements:

Construct a lower triangular complex-valued matrix:

Compute the determinant:

Compute the inverse:

Solve a linear system:

Compute the eigenvalues:

Options  (1)

TargetStructure  (1)

Return the lower triangular matrix as a dense matrix:

Return the lower triangular matrix as a structured array:

Return the lower triangular matrix as a sparse array:

Applications  (2)

A function for computing the LU decomposition of a matrix:

Compute the decomposition:

Verify the decomposition:

Two n×n matrices:

Form a unit lower triangular matrix of size 3n×3n that has the two matrices as blocks:

The n×n lower-left submatrix of the inverse is equivalent to the product of the two original matrices:

Properties & Relations  (2)

Transposing a LowerTriangularMatrix yields an UpperTriangularMatrix:

The entries of a LowerTriangularMatrix are coerced to the lowest precision:

Possible Issues  (1)

A full matrix:

LowerTriangularMatrix[a] does not evaluate if a is not manifestly lower triangular:

Use LowerTriangularMatrix[LowerTriangularize[a]] to get the lower triangular part of a:

Neat Examples  (2)

A Stirling matrix of the first kind:

A Stirling matrix of the second kind:

The two kinds of Stirling matrices are inverses of each other:

A variant of the Pascal matrix with alternating column signs:

Verify that the matrix is involutory (gives the identity matrix when squared):

Wolfram Research (2022), LowerTriangularMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html (updated 2023).

Text

Wolfram Research (2022), LowerTriangularMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html (updated 2023).

CMS

Wolfram Language. 2022. "LowerTriangularMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html.

APA

Wolfram Language. (2022). LowerTriangularMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html

BibTeX

@misc{reference.wolfram_2024_lowertriangularmatrix, author="Wolfram Research", title="{LowerTriangularMatrix}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html}", note=[Accessed: 23-April-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_lowertriangularmatrix, organization={Wolfram Research}, title={LowerTriangularMatrix}, year={2023}, url={https://reference.wolfram.com/language/ref/LowerTriangularMatrix.html}, note=[Accessed: 23-April-2024 ]}