MachinePrecision

MachinePrecision

機械精度を示すために使われる記号である．

詳細

予備知識

  • MachinePrecisionは，機械精度計算において，Wolfram言語のN，NIntegrate，NSum等の数値関数で使われる，小数点以下の桁数を表す記号である．MachinePrecisionの数値は$MachinePrecisionによって与えられる．これは，それ自体が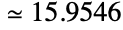に等しい機械精度数である．記号式として使われた場合，MachinePrecisionは値が2進数の53桁精度に相当する53/Log2[10]の厳密な数値として扱われる．
  • 一般に，Wolfram言語の数値関数および画像関数は，計算に使用する所望の数値精度を制御する1つあるいは複数の精度オプションを取る．中でも最もよく使われるオプションに，WorkingPrecision（内部計算で保持すべき精度の桁数を指定）とPrecisionGoal（最終結果で目標とする精度の有効桁数を指定）がある．MachinePrecisionは，すべてのプロット関数とほとんどの数値関数，およびCompile（明示的に呼び出された場合と自動コンパイルの最中に背後で呼び出された場合の両方で）の，デフォルトの作業精度である．
  • 機械精度数（単に「機械数」と呼ばれることも多い）は，常に固定された桁数の数字を持っているが，精度についての情報は保持していない．そのような数についての指数および仮数は別々に保存することができるが，その「スケール」は指数の可能な範囲によって制限されたままである．この種の固定精度数を使った演算は，浮動小数点演算として知られており，IEEE浮動小数点演算標準(IEEE 754)を使って実装されることが多い．機械精度計算は，ネイティブの浮動小数点単位と非常に高速（特に行列演算については高速）であることが多い低レベルの数値ライブラリ操作を使って行われることが多いが，計算中の数値の丸めやその他の要因による精度の低下は記録しない．結果として，機械演算は高速ではあるが，正しい値とは大きく異なる，数値的に有効ではない結果を与える．
  • 機械演算に加え，Wolfram言語は，精度にタグを付けた「任意精度」数を含む「有効数字の計算規則」による演算を許容する．その名前が暗示するように，任意精度数は任意の桁数を含み，結果として，計算を通して伝播できる精度情報を含むことができる．この技術を使うと，最終的な数値結果の精度桁数がもとの数より少ないことがあるが，返された桁は数値的に有効である．
  • MachinePrecisionは，特別な数値化関数Nのデフォルトの精度目標（つまり，最終結果の所望精度）である．ゆえに，N[expr]を使うことは，2引数の形のN[expr,prec]で prec をMachinePrecisionに設定することに等しい．prec を記号のMachinePrecisionに設定することは，数値$MachinePrecisionを設定することとは全く異なることを理解することは重要である．特に，前者は数値化して機械数にするが，後者は指定数の有効桁数を持つ任意精度数に数値化する．例えば，N[Pi,MachinePrecision]とN[Pi,$MachinePrecision]は与える結果が異なる．InputFormまたはFullFormを使ってもとになっている数値表現を見ることができる．これは，機械数では小数点以下が16桁以下であり，任意精度数では digits`prec の形の式である．機械精度あるいは任意精度でもとになっている二進数はRealDigits[expr,2]を使って抽出することができる．
  • 数値に対して明示的な数値精度 prec を指定するときは，数を「バックティック」構文の digits`prec を使って入力する．より一般化すると，SetPrecision[expr,prec]を使ってすべての数が精度 prec を持つような expr を返し，prec が数，MachinePrecisionあるいはInfinityとして指定できるようにすることができる．近似数の0.は特別なケースである．これは，精度を持たず，したがって，たとえ明示的な有限精度を与えられていても，強制的に機械精度に戻される．Precision[expr]を使って指定された式の数値精度を求めることができる．
  • 明示的な桁数の小さい数字を使って指定された数は，機械精度であるとみなされる．つまり，Precision[0.123]はMachinePrecisionを返す．より一般化するなら，近似実数は，$MachinePrecisionより少ない明示的な桁数で入力された場合には，MachinePrecisionで指定された精度を持つものとみなされる．これよりも多い桁数が指定された場合は，その数に指定された桁に対応する精度が割り当てられる（Precision[0.12345678901234567]対Precision[0.123456789012345678]）．
  • 任意精度と機械精度の両方の数を含む計算では，必要に応じてすべての数が強制的に機械精度にされる．さらに，この強制は，任意精度数の精度がMachinePrecisionより小さい場合にも行われる（例：N[E,30] + N[Pi]とN[E,3] + N[Pi]は両方とも機械数を返す）．また，MachinePrecisionを必要とするが，結果の数が53桁を使って表示するには大きすぎるあるいは小さすぎる計算の場合には，結果が自動的に任意精度数として返される（例：N[Exp[1000],MachinePrecision]）．
  • 同じ型の機械精度数と任意精度数は同じHead（例：RealまたはComplex）を持つ．しかし，機械精度数はStandardFormで表示される最大桁数（デフォルトは6桁だが，「環境設定」メニューで変更可）が固定されているのに対し，任意精度数はすべての有意桁を表示する．MachineNumberQ[expr]は，expr が機械精度の実数あるいは複素数であればTrueを返し，それ以外の場合はFalseを返す．数と式を検証するのに役立つその他の関数には，NumberQ，NumericQ，ExactNumberQ，InexactNumberQがある．

例題

すべて開くすべて閉じる

例  (2)

MachinePrecisionは厳密な数値として扱われる：

任意の数と同じように使う：

表現されたビット数：

スコープ  (2)

を近似する機械数：

を機械数と同じ精度で近似する任意精度数：

機械数演算を使って微分方程式を解く：

倍の機械精度を使う：

2つの解を比較する：

アプリケーション  (3)

倍の機械精度に評価する：

関数定義でデフォルト精度の引数に機械精度を使う：

計算が必ず機械数と同じ精度で行われるようにする：

精度を訂正しないと結果の精度が低くなることがある：

特性と関係  (4)

少ない桁数だけを入力した数は機械精度を持つとみなされる：

$MachinePrecision+1よりもたくさんの桁が入力されると，精度は桁数に基づく：

$MachinePrecisionは評価されると数になるのに対し，MachinePrecisionは定数である：

MachinePrecisionは数値的に$MachinePrecisionに等しい(Equal)：

$MachinePrecisionはMachinePrecisionへの機械精度近似である：

MachinePrecision×ビット数÷桁数でバイナリ機械精度が得られる：

既知の精度を超える桁はIndeterminateとして表される：

考えられる問題  (2)

非正規機械数の精度はMachinePrecisionである：

しかし，実際の精度はそれより低く，$MinMachineNumberと同じ不確実性を持つ：

InputFormで入力された非正規機械数の表現不可能な桁は除去される：

任意精度数として入力することですべての桁を保つ：

Wolfram Research (2003), MachinePrecision, Wolfram言語関数， https://reference.wolfram.com/language/ref/MachinePrecision.html.

テキスト

Wolfram Research (2003), MachinePrecision, Wolfram言語関数， https://reference.wolfram.com/language/ref/MachinePrecision.html.

CMS

Wolfram Language. 2003. "MachinePrecision." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MachinePrecision.html.

APA

Wolfram Language. (2003). MachinePrecision. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MachinePrecision.html

BibTeX

@misc{reference.wolfram_2024_machineprecision, author="Wolfram Research", title="{MachinePrecision}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/MachinePrecision.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_machineprecision, organization={Wolfram Research}, title={MachinePrecision}, year={2003}, url={https://reference.wolfram.com/language/ref/MachinePrecision.html}, note=[Accessed: 18-November-2024 ]}