MachinePrecision

MachinePrecision

用以指明机器精度数的精度的一个符号.

更多信息

背景

  • MachinePrecision 是一个表示数字位数的符号，它被用在 Wolfram 语言里进行机器精度计算的如 N、NIntegrate 和 NSum 这些数值函数中，指定它们的计算精度. MachinePrecision 的数值由 $MachinePrecision 给出，后者自身是一个机器精度的数 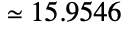. 当被用作符号表达式时，MachinePrecision 被当作值为 53/Log2[10] 的精确数值量，对应的是 53 位的二进制数字精度.
  • 一般情况下，Wolfram 语言中的数值和图形函数都有一个或多个精度选项，用于控制计算所需要的数值精度. 最常见的这类选项是 WorkingPrecision（它指定在内部计算时保持多少位的数值精度）和 PrecisionGoal（它指定了最后的结果有多少位精度的有效数字）. MachinePrecision 是所有绘图函数，大多数数值函数还有 Compile 函数（不论是显式调用还是自动编译时在后台被调用）的默认运算精度的值.
  • 机器精度的数（常简单称作“机器数”）总是有着固定的位数且没有关于精度的信息. 尽管这些数的指数和有效位数可以独立存储，但它们的“数量级”仍然受到指数的可能范围的约束. 采用这种固定精度数字的算术被称为浮点运算，最常见的实现是 IEEE 浮点数算术标准（IEEE 754）. 机器精度的计算通常由专用浮点单元及低层的数值库运算来执行，通常极快（特别是在矩阵算术中），但并没有提供计算过程中可能因为数值舍入或其它因素造成的精度损失的记录以供追索. 这样一来，机器算术给出的是快速但数值上未经验证的结果，可能和正确值有很大的差异.
  • 除了机器算术之外，Wolfram 语言允许用涉及带精度标记的“任意精度”数字的“有效位数算术”来进行数值计算. 正如它们的名字所暗示的，任意精度的数字可以包含任意多位的数字，其结果就是在整个计算过程中都包括精度信息. 使用这一技术，最终返回的数值结果可能比初始输入的精度数字要少，但这些返回的数字是经过数值验证的.
  • MachinePrecision 是特殊数值化函数 N 的默认目标精度（即最终结果需要的精度）. 因此使用 N[expr] 等价于在双参数形式 N[expr,prec] 中把 prec 设定为 MachinePrecision. 重要的是要明白把 prec 设定为符号 MachinePrecision 与设定为数值 $MachinePrecision 完全不同. 特别的，前者是数值化为一个机器数字，而后者是数值化为有指定有效位数的任意精度数字. 例如，N[Pi,MachinePrecision] 和 N[Pi,$MachinePrecision] 给出的结果不同. InputForm 或 FullForm 可被用于查看底层的数值表示，由 16 位或更少的数字组成的就是机器精度的数字而形为 digits`prec 的表达式就是任意精度的数字. 不论是机器精度还是任意精度的数字，它们底层的二进制数字都可以用 RealDigits[expr,2] 释出.
  • 要指定一个数字的显式数值精度 prec，可以用“反勾号”语法 digits`prec 输入数字. 更一般的说，SetPrecision[expr,prec] 可被用于返回 expr 的一个版本，其中所有的数字精度都被设定为 prec，而 prec 可被指定为一个数、MachinePrecision 或 Infinity. 一个特例是近似数 0.，它并不携带精度信息因此总是被强制当作一个机器数，即使显式指定一个有限的精度也是如此. Precision[expr] 可被用于返回指定表达式的数值精度.
  • 用较少位数指定的数字被假设是机器精度的，举例来说就是 Precision[0.123] 返回 MachinePrecision. 更一般而言，近似实数如果输入时的位数少于 $MachinePrecision 就被假设精度为 MachinePrecision. 若指定的位数更多，所输入数字的精度则对应于指定的位数（可比较 Precision[0.12345678901234567] 与 Precision[0.123456789012345678]）.
  • 当有任意精度与机器精度数字同时参与计算时，所有的数都会被粗化为所需要的机器精度. 即便当任意精度数字的指定精度比 MachinePrecision 小时还是会进行这种粗化（例如 N[E,30] + N[Pi] 和 N[E,3] + N[Pi] 返回的都是机器数）. 而且，当计算要求的精度是 MachinePrecision 但最后结果太大或太小从而无法用 53 比特表示时，它会被自动转换为任意精度的数字（例如 N[Exp[1000],MachinePrecision]）.
  • 同样类型的机器精度和任意精度数字都有着同样的 Head（比如 Real 或 Complex）. 然而在 StandardForm 下机器精度的数字最多显示六位数字，而任意精度数字会显示全部有效位数. 若 expr 是机器精度的实数或复数则 MachineNumberQ[expr] 返回 True 否则返回 False. 其它有用的用于测试数字和表达式的函数包括 NumberQ、NumericQ、ExactNumberQ 及 InexactNumberQ.
  • 同一类型的机器精度数和任意精度数具有相同的 Head（即 Real 或 Complex）. 但是，机器精度数以 StandardForm 显示固定数量的最大位数（默认值为 6，但可在 偏好设置 菜单中更改），而任意精度数则显示所有有效数字. 如果 expr 是机器精度实数或复数，MachineNumberQ[expr] 返回 True，否则返回 False. 其他可测试数字和表达式的有用函数包括 NumberQ、NumericQ、ExactNumberQ 和 InexactNumberQ.

范例

打开所有单元关闭所有单元

基本范例  (2)

MachinePrecision 可视为一个精确的数值量：

和其它数字一样使用它：

表示的比特数：

范围  (2)

的机器数近似：

一个任意精度数，它将 近似到与机器数具有相同精度：

用机器数运算求解一个微分方程式：

用两倍的机器精度：

比较以上两个解：

应用  (3)

计算到两倍机器精度：

在一个函数定义中使用机器精度作为缺省的精度参数：

确保计算的执行是用跟机器数一样的精度：

如果不固定精度，产生结果精度可能较低：

属性和关系  (4)

输入只有较少几位数字的数时，它被视为具有机器精度：

当输入大于 $MachinePrecision+1 位数的数字时，精度取决于输入的位数：

MachinePrecision 是一个数值常量，而 $MachinePrecision 计算为一个数：

MachinePrecision 在数值上等于(Equal) $MachinePrecision：

$MachinePrecision 是 MachinePrecision 的机器精度近似：

MachinePrecision 乘以每位数字的比特数得到二进制的机器精度：

超过已知精度的数字表示为 Indeterminate：

可能存在的问题  (2)

非规范机器数的精度为 MachinePrecision：

但是，它们的实际精度要更小，且不准确度与 $MinMachineNumber 相同：

以 InputForm 形式输入的非规范机器数将丢弃不可表示的数字：

按任意精度数输入，保留所有数字：

Wolfram Research (2003)，MachinePrecision，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MachinePrecision.html.

文本

Wolfram Research (2003)，MachinePrecision，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MachinePrecision.html.

CMS

Wolfram 语言. 2003. "MachinePrecision." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MachinePrecision.html.

APA

Wolfram 语言. (2003). MachinePrecision. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MachinePrecision.html 年

BibTeX

@misc{reference.wolfram_2024_machineprecision, author="Wolfram Research", title="{MachinePrecision}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/MachinePrecision.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_machineprecision, organization={Wolfram Research}, title={MachinePrecision}, year={2003}, url={https://reference.wolfram.com/language/ref/MachinePrecision.html}, note=[Accessed: 18-November-2024 ]}