MardiaKurtosisTest

MardiaKurtosisTest[data]

Mardia尖度検定を使って data がMultinormalDistributionに従うかどうかを調べる．

MardiaKurtosisTest[data,"property"]

"property"の値を返す．

詳細とオプション

  • MardiaKurtosisTestは data がMultinormalDistributionから引き出されたという帰無仮説 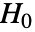とそうではないという対立仮説 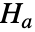でMardia尖度の適合度検定を行う．
  • デフォルトで，確率値つまり 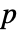値が返される．
  • 小さい 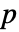値は data が正規分布に従っている可能性が低いことを示す．
  • data は一変量{x1,x2,…}あるいは多変量{{x1,y1,…},{x2,y2,…},…}でよい．
  • Mardia尖度検定は事実上 data の尖度の多変量基準をMultinormalDistributionと比べる．
  • MardiaKurtosisTest[data,dist,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる．
  • MardiaKurtosisTest[data,dist,"property"]を使って直接"property"の値を与えることができる．
  • PearsonChiSquareTest[data,dist,"property"]を使って直接"property"の値を与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定で使用する自由度
    "PValue" 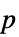値
    "PValueTable""PValue"のフォーマットされたバージョン
    "ShortTestConclusion"検定結果の簡単な説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 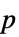値
    "TestDataTable""TestData"のフォーマットされたバージョン
    "TestStatistic"検定統計
    "TestStatisticTable""TestStatistic"のフォーマットされたバージョン
  • 次の特性はどの検定が行われているかに依存しない．
  • データ分布に関連する特性
  • "FittedDistribution"データのフィットした分布
    "FittedDistributionParameters"データの分布母数
  • 使用可能なオプション
  • Method Automatic 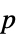値を計算するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
  • 適合度検定では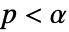， のときにのみ 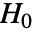が棄却されるような切捨て 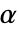が選択される．特性"TestConclusion"および"ShortTestConclusion"で使われる 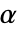の値はSignificanceLevelオプションで制御される．デフォルトで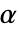， は0.05に設定されている．
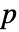  • 値の計算に次のメソッドを使うことができる．
  • Automatic五次元までの小さいサンプルについて修正する
    "Asymptotic"検定統計の漸近的な分布を使う
    "MonteCarlo"モンテカルロ(Monte Carlo)シミュレーションを使う
  • Method->"MonteCarlo"の設定では，入力 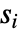と同じ長さの 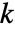個のデータ集合がフィットされた分布を使って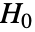，のもとで生成される．次に，"MonteCarlo"からのEmpiricalDistribution，MardiaKurtosisTest[si,"TestStatistic"]を使って 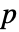値が推定される．

例題

すべて開くすべて閉じる

例  (3)

多変量の正規性の検定を行う：

Mardiaの尖度検定から検定統計を抽出する：

フォーマットされた検定表を得る：

スコープ  (5)

検定  (2)

多変量の正規性についてMardiaの尖度検定を行う：

正規データの 値は，非正規データの 値と比べて大きい：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

レポート  (3)

Mardiaの尖度検定の結果を表にする：

完全な検定表：

値の表：

検定統計：

カスタマイズされたレポート用にMardiaの尖度検定の表から項目を取り出す：

"ShortTestConclusion"と"TestConclusion"を使って検定の結論をレポートする：

有意水準が異なると，結論も異なることがある：

オプション  (4)

Method  (3)

モンテカルロ(Monte Carlo)法に基づくメソッドあるいは計算式を使う：

モンテカルロ法に基づくメソッドで使うサンプル数を設定する：

モンテカルロ推定は，サンプルを増やすと，真の 値に収束する：

モンテカルロ法に基づくメソッドで使われるランダムなシードを設定する：

シードは生成器の状態に影響を与え，結果の 値にもいくらか影響を与える：

SignificanceLevel  (1)

"TestConclusion"と"ShortTestConclusion"で使う有意水準を設定する：

デフォルトで0.05が使われる：

アプリケーション  (2)

Mardiaの尖度検定の検出力曲線：

近似検出力曲線を可視化する：

基礎となる分布がMultivariateTDistributionであり，検定サイズが0.05，サンプルサイズが27である場合に，Mardiaの尖度検定の検出力を推定する：

3種のアヤメについて花弁と萼片の大きさを記録した．2つの似た種を区別するのに便利かもしれない尺度を素早くチェックするために，平均の多変量検定が使えるが，これはデータが多変量の正規分布に従う場合にのみ有効である：

2種の多変量尖度は多変量正規分布に似ている：

多変量歪度も正規性を確認するためにチェックすべきである：

データは正規性を持つようであるので，TTestは有効である：

特性と関係  (5)

多変量検定統計：

一変量検定統計：

多変量検定統計は，漸近的なNormalDistribution[0,1]に従う：

漸近的な 値は小さいサンプルにおいては全く不正確であることもある：

これに比べてモンテカルロの 値は，小さいサンプルの値にずっと近い：

Mardiaの尖度検定は，正規性からの逸脱を尖度でのみ検出できる：

データは明らかに正規分布に従っていない：

決定はMardiaSkewnessTestとMardiaKurtosisTestに基づくべきである：

Mardia尖度検定は，入力がTimeSeriesのときにのみ値に使うことができる：

考えられる問題  (1)

データの共分散行列が正定値でなければ，検定は失敗に終る：

データ点の数は，データの次元よりも大きくなければならない：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説によって与えられる検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), MardiaKurtosisTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html.

テキスト

Wolfram Research (2010), MardiaKurtosisTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html.

CMS

Wolfram Language. 2010. "MardiaKurtosisTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html.

APA

Wolfram Language. (2010). MardiaKurtosisTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html

BibTeX

@misc{reference.wolfram_2024_mardiakurtosistest, author="Wolfram Research", title="{MardiaKurtosisTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mardiakurtosistest, organization={Wolfram Research}, title={MardiaKurtosisTest}, year={2010}, url={https://reference.wolfram.com/language/ref/MardiaKurtosisTest.html}, note=[Accessed: 22-November-2024 ]}