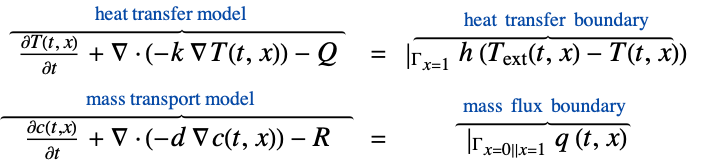MassFluxValue
MassFluxValue[pred,vars,pars]
represents a mass flux boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassFluxValue[pred,vars,pars,lkey]
represents a mass flux boundary condition with local parameters specified in pars[lkey].
Details



- MassFluxValue specifies a boundary condition for MassTransportPDEComponent and is used as part of the modeling equation:
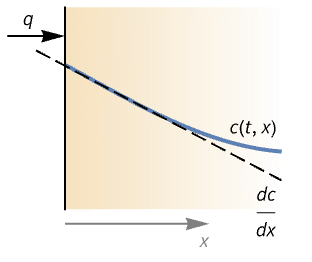
- MassFluxValue is typically used to model mass species flow through a boundary caused by a species source or sink outside of the domain.
- A flow rate is the flow of a quantity like energy or mass per time. Flux is the flow rate through the boundary and is measured in the units of the quantity per area per time. A millimeter of rain per cross section of opening area per hour is a rain flux.
- MassFluxValue models the rate of mass species flowing through some part of the boundary with dependent variable
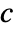 in [
in [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassFluxValue.en/4.png) ], independent variables
], independent variables 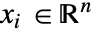 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassFluxValue.en/6.png) ] and time variable
] and time variable 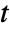 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassFluxValue.en/8.png) ].
]. - Stationary variables vars are vars={c[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={c[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative time-dependent mass transport model MassTransportPDEComponent is based on a convection-diffusion model with mass diffusivity
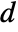 , mass convection velocity vector
, mass convection velocity vector 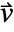 , mass reaction rate
, mass reaction rate 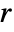 and mass source term
and mass source term 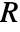 :
: - The conservative time-dependent mass transport model MassTransportPDEComponent is based on a conservative convection-diffusion model given by:
- In the non-conservative form, MassFluxValue with mass flux
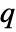 in
in 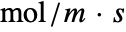 and boundary unit normal
and boundary unit normal 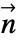 models:
models: - In the conservative form, MassFluxValue models:
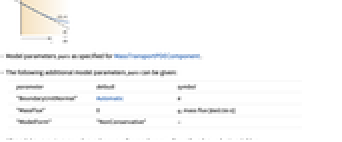
- Model parameters pars as specified for MassTransportPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "BoundaryUnitNormal" Automatic 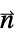
"MassFlux" - 0
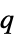 , mass flux [
, mass flux [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , "m", , "s", , ")"}, moles per meter second, {{(, "Moles", )}, /, {(, {"Meters", , "Seconds"}, )}}}, QuantityTF]](Files/MassFluxValue.en/23.png) ]
]"ModelForm" "NonConservative" - - All model parameters may depend on any of
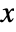 ,
, 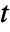 and
and 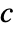 , as well as other dependent variables.
, as well as other dependent variables. - To localize model parameters, a key lkey can be specified, and values from association pars[lkey] are used for model parameters.
- MassFluxValue evaluates to a NeumannValue.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MassFluxValue depends on parameters
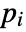 that are specified in the association pars as …,keypi…,pivi,…], the parameters
that are specified in the association pars as …,keypi…,pivi,…], the parameters 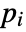 are replaced with
are replaced with 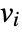 .
.

Examples
open allclose allBasic Examples (2)
Scope (10)
Basic Examples (2)
1D (1)
Model a 1D chemical species field in an incompressible fluid whose right side and left side are subjected to a mass concentration and inflow condition, respectively:
Set up the stationary mass transport model variables ![]() :
:
Specify the mass transport model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Specify a species flux boundary condition:
2D (1)
Model mass transport of a pollutant in a 2D rectangular region in an isotropic homogeneous medium. Initially, the pollutant concentration is zero throughout the region of interest. A concentration of 3000 ![]() is maintained at a strip with dimension 0.2
is maintained at a strip with dimension 0.2 ![]() located at the center of the left boundary, while the right boundary is subject to a parallel species flow with a constant concentration of 1500
located at the center of the left boundary, while the right boundary is subject to a parallel species flow with a constant concentration of 1500 ![]() , allowing for mass transfer. A pollutant outflow of 100
, allowing for mass transfer. A pollutant outflow of 100 ![]() is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833
is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833 ![]() is distributed uniformly with a uniform horizontal velocity of 0.01
is distributed uniformly with a uniform horizontal velocity of 0.01 ![]() :
:
Set up the mass transport model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Set up a species concentration source of 0.2 ![]() length at the center of the left surface:
length at the center of the left surface:
Set up a mass transfer boundary on the right surface:
3D (1)
Model a non-conservative chemical species field in a unit cubic domain, with two mass conditions at two lateral surfaces and a mass inflow through a circle with radius 0.2 ![]() at the center of the top surface, as well as an orthotropic mass diffusivity
at the center of the top surface, as well as an orthotropic mass diffusivity ![]() :
:
Set up the mass transport model variables ![]() :
:
Specify a diffusivity ![]() and a flow velocity field
and a flow velocity field ![]() :
:
Specify a flux condition ![]() of
of ![]() through a regional circle on the top surface:
through a regional circle on the top surface:
Material Regions (1)
Model a 1D chemical species transport through different material with a reaction rate in one. The right side and left side are subjected to a mass concentration and inflow condition, respectively:
Set up the stationary mass transport model variables ![]() :
:
Specify the mass transport model parameters species diffusivity ![]() and a reaction rate
and a reaction rate ![]() active in the region
active in the region ![]() :
:
Specify a species flux boundary condition:
Time Dependent (1)
Model a 1D non-conservative chemical species field and a mass flux through part of the boundary with:
Set up the time-dependent mass transport model variables ![]() :
:
Specify the mass transport model parameters mass diffusivity ![]() and mass convection velocity
and mass convection velocity ![]() :
:
Set up the equation with a mass flux ![]() of
of ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Solve the PDE with an initial condition of a zero concentration:
Nonlinear Time Dependent (1)
Model a 1D non-conservative chemical species field with a nonlinear diffusivity coefficient ![]() and an outflow condition through part of the boundary, which is expressed as follows:
and an outflow condition through part of the boundary, which is expressed as follows:
Set up the mass transport model variables ![]() :
:
Specify a nonlinear species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Specify an outflow flux ![]() of
of ![]() applied at the right end:
applied at the right end:
Specify a time-dependent mass concentration surface condition:
Coupled Time Dependent (2)
Model a 1D coupled non-conservative dual chemical species field with corresponding mass flux through the left parts of the boundary:
Set up the time dependent mass transport model variables ![]() for the
for the ![]() and
and ![]() species, respectively:
species, respectively:
Specify the mass transport model parameters mass diffusivity ![]() and
and ![]() for the
for the ![]() and
and ![]() species:
species:
Set up the boundary conditions with a mass flux ![]() of
of ![]() and
and ![]() for
for ![]() and
and ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Model a 1D coupled chemical species field with a convection velocity and a mass flux through the left boundary:
Set up the time-dependent mass transport model variables ![]() for
for ![]() and
and ![]() species, respectively:
species, respectively:
Specify the mass transport model parameters mass diffusivity ![]() and
and ![]() for the
for the ![]() and
and ![]() species:
species:
Set up the equation with a mass flux ![]() of 6
of 6 ![]() and 12
and 12 ![]() for
for ![]() and
and ![]() at the left end for the first 50 seconds:
at the left end for the first 50 seconds:
Applications (2)
Single Equation (1)
Model mass transport of a pollutant in a 2D rectangular region in an isotropic homogeneous medium. Initially, the pollutant concentration is zero throughout the region of interest. A concentration of 3000 ![]() is maintained at a strip with dimension 0.2
is maintained at a strip with dimension 0.2 ![]() located at the center of the left boundary, while a pollutant outflow of 100
located at the center of the left boundary, while a pollutant outflow of 100 ![]() is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833
is applied at both the top and bottom boundaries. A diffusion coefficient of 0.833 ![]() is distributed uniformly, but both horizontal and vertical velocity are spatial dependent:
is distributed uniformly, but both horizontal and vertical velocity are spatial dependent:
Set up the mass transport model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify model parameters species diffusivity ![]() and fluid flow velocity
and fluid flow velocity ![]() :
:
Set up a species concentration source of 0.2 ![]() length at the center of the left surface:
length at the center of the left surface:
Coupled Equations (1)
Solve a coupled heat transfer and mass transport model with a thermal transfer value and a mass flux value on the boundary:
Set up the heat transfer mass transport model variables ![]() :
:
Specify heat transfer and mass transport model parameters, heat source ![]() , thermal conductivity
, thermal conductivity ![]() , mass diffusivity
, mass diffusivity ![]() and mass source
and mass source ![]() :
:
Specify boundary condition parameters for a thermal convection value with an external flow temperature ![]() of 1000 K and a heat transfer coefficient
of 1000 K and a heat transfer coefficient ![]() of
of ![]() :
:
Text
Wolfram Research (2020), MassFluxValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MassFluxValue.html.
CMS
Wolfram Language. 2020. "MassFluxValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassFluxValue.html.
APA
Wolfram Language. (2020). MassFluxValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassFluxValue.html