MassSymmetryValue
MassSymmetryValue[pred,vars,pars]
represents a mass symmetry boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
MassSymmetryValue[pred,vars,pars,lkey]
represents a mass symmetry boundary condition with local parameters specified in pars[lkey].
Details


- MassSymmetryValue specifies a boundary condition for MassTransportPDEComponent and is used as part of the modeling equation:
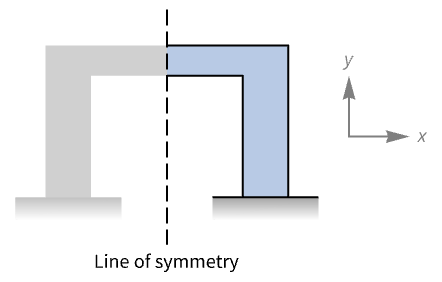
- MassSymmetryValue is typically used to model a boundary with mirror symmetry along an axis.
- MassSymmetryValue models a boundary with mirror symmetry with dependent variable
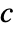 in [
in [![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassSymmetryValue.en/4.png) ], independent variables
], independent variables 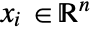 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassSymmetryValue.en/6.png) ] and time variable
] and time variable 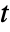 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassSymmetryValue.en/8.png) ].
]. - Stationary variables vars are vars={c[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={c[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative-time dependent mass transport model MassTransportPDEComponent is based on a convection-diffusion model with mass diffusivity
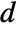 , mass convection velocity vector
, mass convection velocity vector 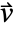 , mass reaction rate
, mass reaction rate 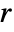 and mass source term
and mass source term 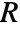 :
: - The conservative time-dependent mass transport model MassTransportPDEComponent is based on a conservative convection-diffusion model given by:
- The normal flow velocity
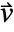 on the symmetry boundary will remain at zero at all times.
on the symmetry boundary will remain at zero at all times. - Both in the conservative and non-conservative forms, MassSymmetryValue with boundary unit normal
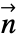 models:
models: - Model parameters pars as specified for MassTransportPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "ModelForm" "NonConservative" 
- MassSymmetryValue is effectively the same as MassFluxValue with a heat flux of 0.
- The boundary predicate pred can be specified as in NeumannValue.
- If the MassSymmetryValue depends on parameters
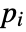 that are specified in the association pars as …,keypi…,pivi,…], the parameters
that are specified in the association pars as …,keypi…,pivi,…], the parameters 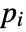 are replaced with
are replaced with 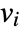 .
.
Examples
Basic Examples (3)
Set up a mass symmetry boundary condition:
Set up a system of mass symmetry boundary conditions:
Symmetry boundaries can be used to reduce the size of the geometry of the model. Set up a mass transport equation:
Set up and visualize a region:
Solve and visualize the equation:
Set up a region about the symmetry axis at ![]() :
:
Solve and visualize the equation with a symmetry boundary at ![]() :
:
Text
Wolfram Research (2020), MassSymmetryValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MassSymmetryValue.html.
CMS
Wolfram Language. 2020. "MassSymmetryValue." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MassSymmetryValue.html.
APA
Wolfram Language. (2020). MassSymmetryValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassSymmetryValue.html