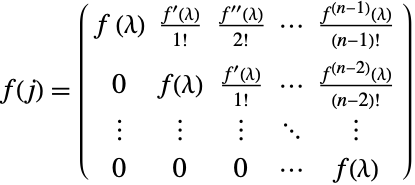MatrixFunction

MatrixFunction[f,m]

给出标量函数 f 对矩阵参数 m 生成的矩阵.

更多信息和选项

  • 矩阵函数把一个矩阵转化为另一个矩阵. 对于收敛幂级数，MatrixFunction[f,m] 事实上计算函数 f 的由矩阵幂替换的原始幂的幂级数. »
  • 函数 f 应该是一元可微的或者符号式函数.
  • MatrixFunction 只可用于方阵. 对于精确和符号式矩阵，它对于不精确矩阵和约旦方法应用 Schur–Parlett方法.
  • MatrixFunction 可用于 SparseArray 对象和结构化数组.
  • 可以给出 Method 选项，具有可能的显示设置：
  • "Jordan"约旦分解
    "Schur"使用块 Parlett 迭代的舒尔分解
  • "Schur" 方法可以使用方法选项 mopts 通过 Method->{"Schur",mopts} 指定. 可以给出下列方法选项：
  • "Balanced"False是否在舒尔分解前平衡输入矩阵
    "BlockSeparationDelta"Automatic在单个 Parlett 块中相邻特征值之间的最大分割

范例

打开所有单元关闭所有单元

基本范例  (3)

计算符号矩阵的平方根：

验证它确实是平方根：

注意，这与简单地计算每个项的平方根不同：

计算 3×3 矩阵 m 的对数：

验证结果的指数是原始矩阵：

对矩阵多项式进行计算，将多项式指定为纯函数：

范围  (11)

基本用法  (7)

计算机器精度矩阵的矩阵正弦和余弦：

测试矩阵恒等式 ：

计算复矩阵的矩阵正弦：

计算一个精确矩阵的平方根：

用 20 位精度的算术计算一个多项式的对数的矩阵函数：

计算对角符号矩阵的矩阵正弦：

计算非对角符号矩阵的矩阵正切：

用符号标量函数计算矩阵函数：

用符号标量函数计算符号矩阵：

可高效地对机器精度的矩阵应用函数：

特殊矩阵  (4)

对稀疏矩阵计算矩阵函数通常会产生一个正常矩阵：

对结构化数组计算矩阵多项式：

将矩阵函数应用于单位矩阵只改变对角元素的值：

更广义的说，对任何对角矩阵应用函数都只作用于其对角元素：

以 20 位的精度计算 HilbertMatrix 的平方：

选项  (4)

Method  (4)

"Jordan" 方法适用于精确和非精确矩阵：

"Schur" 方法只适用于非精确（机器精度和任意精度）矩阵：

如果许多特征值非常接近，则将它们放入分块对角子矩阵中，子矩阵可能会变大；然后计算成本更高，收敛速度可能很慢：

"BlockSeparationDelta" 取较小的值，可减小对角块的大小，同时加快收敛速度：

但是结果可能更不准确：

当输入矩阵的平衡状态不好（包括幅值差别很大的项），平衡可能改善结果：

应用  (5)

求应用于特定向量的矩阵幂的第二个逆：

这是计算 的更有效的方法：

证明一个矩阵是其特征多项式的根：

对于标量符号 ，，， 的解如下给出：

如果 是一个矩阵，解可以在标量解中使用矩阵函数计算：

求满足 的矩阵：

对于由矩阵 的单链组成的 Jordan 矩阵，确认公式 ：

属性和关系  (11)

使用函数 1& 将返回一个单位矩阵：

使用函数 1/#& 与使用 Inverse 相同:

使用具有幂的函数等价于使用 MatrixPower:

MatrixFunction[Exp,m] 本质上等同于 MatrixExp[m]：

MatrixFunction 实际上使用的是幂级数，用 MatrixPower 替换 Power：

与 一样，MatrixExp[MatrixFunction[Log,m]] 等于 m：

如果 m 是对角矩阵，MatrixFunction[f,m] 只对 m 的对角线上的元素应用 f：

如果 m 是上三角矩阵，则 MatrixFunction[f,m] 也是上三角矩阵：

类似的陈述对下三角矩阵同样成立：

如果 使用 进行对角化处理，并且特征向量的条件良好，那么 :

可从 JordanDecomposition 计算 ，即 v.f(j).TemplateBox[{v}, Inverse]：

而且， 为零，除了超对角元中由 1 划定的上三角块中的元素：

矩阵是特征多项式的根：

可能存在的问题  (4)

对于精确或者符号式矩阵，标量函数可以具有符号式导数：

与这个例子比较：

MatrixFunction 不可用于不可导函数诸如 Abs:

它将对精确输入矩阵返回矩阵函数，但是结果没有意义，因为 Abs 不具有一阶或者二阶导数：

当在矩阵特征值处没有定义标量函数或者它的初始导数，MatrixFunction 不返回结果：

标量函数 f 具有极点（奇异点）位于 1、2 和 3:

如果标量函数不是解析的并且矩阵特征值接近函数极点，那么所得矩阵常常是不正确的：

巧妙范例  (1)

Wolfram Research (2012)，MatrixFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MatrixFunction.html （更新于 2014 年）.

文本

Wolfram Research (2012)，MatrixFunction，Wolfram 语言函数，https://reference.wolfram.com/language/ref/MatrixFunction.html （更新于 2014 年）.

CMS

Wolfram 语言. 2012. "MatrixFunction." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/MatrixFunction.html.

APA

Wolfram 语言. (2012). MatrixFunction. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MatrixFunction.html 年

BibTeX

@misc{reference.wolfram_2024_matrixfunction, author="Wolfram Research", title="{MatrixFunction}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixFunction.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_matrixfunction, organization={Wolfram Research}, title={MatrixFunction}, year={2014}, url={https://reference.wolfram.com/language/ref/MatrixFunction.html}, note=[Accessed: 22-November-2024 ]}