MeanShift

MeanShift[list,d]

list 中の各要素を差が d より小さいすべての要素の値の平均で置換する．

MeanShift[list,d,{p1,p2,…}]

指定された部分 piのみが平均値シフトされた値で置換されたリストを返す．

MeanShift[image,…]

image における画素値の平均値シフト．

詳細とオプション

  • MeanShiftは，モード探究法としても知られており，一般にデータ配列や画像の平滑化に使われる．
  • MeanShiftは，入力要素の順序を保存する．
  • MeanShift[image,d,parts]では，parts はマーカー画像あるいは{row,column}位置のリストでよい．
  • 使用可能なオプション
  • DistanceFunction EuclideanDistance距離計量関数
    MaxIterations 1最大反復回数
    Tolerance 0収束を想定するのに許される許容量
    Weights Automatic平均値を計算するために使われる重み
  • Tolerance->t のとき，平均値シフト反復は，どの点も t より大きく変わらなくなると停止する．
  • デフォルトでは単位重みが使われる．Weights->f を使うと，要素間の再スケールされた距離に適用された関数 f が値の重み付き平均値を計算して返すために使われる．0から d までの距離は，0から1の範囲になるように再スケールされる．
  • Weightsのよく使われる設定値
  • UnitStep単位重み（デフォルト）
    UnitTriangle線形に減少する重み
    "Gaussian"シグマ 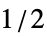のガウス窓に基づく重み
    {"Gaussian",σ}シグマ σ のガウス窓
  • DistanceFunctionオプションによく使われる設定値
  • ManhattanDistanceマンハッタン距離すなわち「市街地」距離
    EuclideanDistanceユークリッド距離
    SquaredEuclideanDistanceユークリッド距離の二乗
    NormalizedSquaredEuclideanDistance正規化されたユークリッド距離の二乗
    CosineDistance角コサイン距離
    CorrelationDistance相関係数距離
    f任意の関数 f を使う

例題

すべて開くすべて閉じる

例  (3)

整数のリストの平均値シフト：

ベクトルのリストの平均値シフト：

複数回反復した後の，画像の画素の平均値シフト：

スコープ  (4)

データ集合から一様ノイズを除去する：

記号式に適用された平均値シフトアルゴリズム：

点の部分集合に適用された，平均値シフトアルゴリズム：

入力精度は保たれている：

オプション  (8)

DistanceFunction  (3)

デフォルトで，EuclideanDistanceが使われる：

距離関数を指定する：

カスタムの距離関数を使う：

MaxIterations  (2)

デフォルトで，平均値シフトの反復は，入力には1回しか適用されない：

MaxIterationsを使って反復回数を指定する：

MaxIterations->Infinityを使って収束するまで実行する：

MaxIterationsを使って反復しながらデータを平滑化する：

Tolerance  (1)

デフォルトで，ゼロ許容度が使われる：

許される許容度を指定する：

Weights  (2)

デフォルトで，一様重みが使われる：

各サンプルからの距離に基づいて，近傍に線形に重みを付ける：

各サンプルからの距離の二乗に基づいて，近傍に指数的に重みを付ける：

色分割のための"Gaussian"重み：

デフォルトの一様重みで：

アプリケーション  (9)

平滑化  (2)

ノイズの多いデータ集合の大規模特徴を求める：

結合された空間範囲領域における，5D特徴の平均値シフトを使った画像の平滑化：

色距離の計算に適したLABColor値を使う：

範囲を0から1までに正規化した空間位置特徴を計算する：

画素の色と位置から5D特徴を構築する：

"Gaussian"重みとEuclideanDistanceを使って平均値シフトのフィルタリングを1回反復する．これは，ガウス重みの付いた空間と範囲の特徴を掛けることに等しい：

フィルタがかかった色の値を使って出力画像を作成する：

10回反復する：

平均値シフト移動  (2)

1D平均値シフトベクトルを計算する：

単峰型2Dデータを生成する：

峰に向かって繰り返し上昇する点の軌跡を計算する：

連続する平均値シフトベクトルのノルムと方向を可視化する：

上昇を可視化する：

推定分布の峰を求める  (1)

0，2，4の三峰分布からサンプルデータを得る：

データをモザイクにするサンプルが収束するまで平均値シフトを適用する：

摂動する位置から平均値シフトを再開することで，もとになっている確率密度関数の極大値ではない点を削り取る：

近くのピークを集めることで峰を求める：

クラスタリング  (2)

分布からデータを生成する：

すべてのデータ点が収束するまで平均値シフトを適用する：

結果を集めてクラスタにする：

クラスタリングを可視化する：

分布から大量のデータを生成する：

データサンプルのほんの一部について，軌跡を計算する：

互いの半径内で終る経路をまとめる：

各軌道にラベルを付け，対応する最近点関数を計算する：

ラベルの付いていない各サンプルに，最も近い軌道のラベルが割り当てられる：

クラスタリングを可視化する：

データ集合全体が収束するまで平均値シフトを計算するのには時間がかかる：

画像分割  (2)

"LAB"色成分の3D 特徴空間で平均値フィルタリングを繰り返す：

5D空間範囲特徴領域で平均値フィルタリングを実行する：

特徴値が半径よりも少ししか離れていない成分をまとめる：

最終分割と量子化された画像を計算する：

特性と関係  (3)

リストの一部に平均値シフトを行う：

平均値シフトされた要素を抽出する：

画像の一部に平均値シフトを行う：

最初に検出された明るい成分のマスクを作成する：

平滑化する：

平均値シフトされた画素値を抽出する：

平均値シフトベクトルは，密度推定によって正規化された勾配密度推定に比例する：

おもしろい例題  (1)

平均値シフトの繰返しを示す：

Wolfram Research (2010), MeanShift, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeanShift.html （2014年に更新）.

テキスト

Wolfram Research (2010), MeanShift, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeanShift.html （2014年に更新）.

CMS

Wolfram Language. 2010. "MeanShift." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MeanShift.html.

APA

Wolfram Language. (2010). MeanShift. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanShift.html

BibTeX

@misc{reference.wolfram_2024_meanshift, author="Wolfram Research", title="{MeanShift}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MeanShift.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_meanshift, organization={Wolfram Research}, title={MeanShift}, year={2014}, url={https://reference.wolfram.com/language/ref/MeanShift.html}, note=[Accessed: 22-November-2024 ]}