MeanShiftFilter

MeanShiftFilter[data,r,d]

filters data by replacing every value by the mean of the pixels in a range-r neighborhood and whose value is within a distance d.

MeanShiftFilter[data,{r1,r2,…},d]

uses ri for filtering the ^(th)dimension in data.

Details and Options

  • MeanShiftFilter is used to locally smooth data and diminish noise while preserving significant jumps such as edges in images, where the amount of smoothing is dependent on the values of r and d.
  • The function applied to each range-r neighborhood is MeanShift.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries, TemporalData, …
    imagearbitrary Image or Image3D object
    audioan Audio object
  • For multichannel images and audio signals, the distance is computed between channel vectors.
  • MeanShiftFilter[data,{r1,r2,…},d] computes the mean shift value in 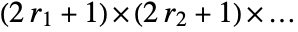blocks centered on each sample.
  • MeanShiftFilter assumes the index coordinate system for lists and images.
  • At the data boundaries, MeanShiftFilter uses smaller neighborhoods.
  • The following options can be given:
  • DistanceFunction EuclideanDistancehow to compute the distance between values
    MaxIterations 1maximum number of iterations to be performed
  • For a complete list of possible settings for DistanceFunction, see the reference page for MeanShift.
  • The possible range for the distance parameter d depends on the distance function as well as the dimension of the color space.

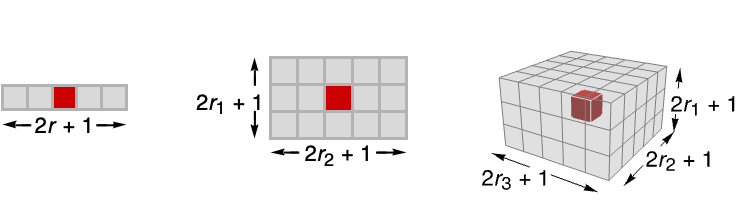
Background & Context

Examples

open allclose all

Basic Examples  (3)

Mean-shift filtering of a vector:

Filter a TimeSeries:

Mean-shift filtering of a color image:

Scope  (11)

Data  (6)

Mean-shift filtering of data:

Mean-shift filtering of a 2D array:

Filter a TimeSeries:

Filter an Audio signal:

Mean-shift filtering of a grayscale image:

Mean-shift filtering of a 3D image:

Parameters  (5)

Specify one radius to be used in all directions:

Mean-shift filtering in just the first direction:

Filtering in just the second direction:

Mean-shift filtering of a 3D image in the vertical direction only:

Mean-shift filtering of a 3D image in the horizontal planes only:

Mean-shift filter averages only over pixels that differ in value by less than d:

Options  (3)

DistanceFunction  (2)

By default, EuclideanDistance is used:

Specify the distance function:

MaxIterations  (1)

By default, only one iteration of mean shift is applied to input:

Use MaxIterations to specify the number of iterations:

Applications  (2)

Use mean-shift filtering to smooth an image while preserving the edges:

Use mean-shift filtering as a preprocessing step for image segmentation:

Properties & Relations  (1)

MeanShiftFilter is equivalent to MeanFilter for distance d greater than the data dynamic range:

Neat Examples  (1)

Show how MeanShiftFilter iteratively shifts values until they converge:

Wolfram Research (2010), MeanShiftFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/MeanShiftFilter.html (updated 2016).

Text

Wolfram Research (2010), MeanShiftFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/MeanShiftFilter.html (updated 2016).

CMS

Wolfram Language. 2010. "MeanShiftFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MeanShiftFilter.html.

APA

Wolfram Language. (2010). MeanShiftFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeanShiftFilter.html

BibTeX

@misc{reference.wolfram_2025_meanshiftfilter, author="Wolfram Research", title="{MeanShiftFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MeanShiftFilter.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_meanshiftfilter, organization={Wolfram Research}, title={MeanShiftFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/MeanShiftFilter.html}, note=[Accessed: 18-April-2025 ]}