MeanShift
更多信息和选项


- MeanShift 也称为模式搜寻,并且通常用于数据数组和图像的平滑处理.
- MeanShift 保持输入元素的顺序.
- 在 MeanShift[image,d,parts] 中,parts 可以是一个记号图像或者 {row,column} 位置列表.
- 可以给出下列选项:
-
DistanceFunction EuclideanDistance 距离度量函数 MaxIterations 1 执行的最大迭代次数 Tolerance 0 假定收敛性允许的容差 Weights Automatic 用于计算均值的权值 - 设置 Tolerance->t 时,如果没有点改变超过 t 时迭代停止.
- 默认情况下,使用单位权值. 使用 Weights->f,应用于元素之间的可调节尺寸的距离的函数 f 用于计算和返回数值的加权均值. 0和 d 之间的距离缩放到范围0和1之间.
- Weights 的典型设置包括:
-
UnitStep 单位权值(默认) UnitTriangle 线性递减权值 "Gaussian" 基于具有 sigma 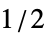 的高斯窗的权值
的高斯窗的权值{"Gaussian",σ} 具有 sigma σ 的高斯窗 - 通常将 DistanceFunction 选项设置为:
-
ManhattanDistance 曼哈顿或者“市街区”距离 EuclideanDistance 欧几里得距离 SquaredEuclideanDistance 平方欧几里得距离 NormalizedSquaredEuclideanDistance 归一化的平方欧几里得距离 CosineDistance 角余弦距离 CorrelationDistance 相关系数距离 f 使用任意函数 f
范例
打开所有单元 关闭所有单元选项 (8)
DistanceFunction (3)
MaxIterations (2)
应用 (9)
平滑 (2)
使用联合空间范围区域中五维特征的均值漂移,对图像进行平滑处理:
使用 LABColor 数值,适用于计算颜色距离:
使用 "Gaussian" 权值和 EuclideanDistance 执行均值漂移的一次迭代,等价于对高斯权值的空间和范围特征加倍:
求估计分布的模式 (1)
聚类 (2)
属性和关系 (3)
文本
Wolfram Research (2010),MeanShift,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MeanShift.html (更新于 2014 年).
CMS
Wolfram 语言. 2010. "MeanShift." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/MeanShift.html.
APA
Wolfram 语言. (2010). MeanShift. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MeanShift.html 年
BibTeX
@misc{reference.wolfram_2025_meanshift, author="Wolfram Research", title="{MeanShift}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MeanShift.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_meanshift, organization={Wolfram Research}, title={MeanShift}, year={2014}, url={https://reference.wolfram.com/language/ref/MeanShift.html}, note=[Accessed: 27-February-2026]}

