WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

TrimmedMean
✖
TrimmedMean

Updated in 14.1

✖
TrimmedMean[list,f]

gives the mean of the elements in list after dropping a fraction f of the smallest and largest elements.

✖
TrimmedMean[list,{f1,f2}]

gives the mean when a fraction f1 of the smallest elements and a fraction f2 of the largest elements are removed.

✖
TrimmedMean[list]

gives the 5% trimmed mean TrimmedMean[list,0.05].

✖
TrimmedMean[dist,…]

gives the trimmed mean of a univariate distribution dist.

Details

  • TrimmedMean gives a robust estimate of the mean by excluding extreme values.
  • The trimming fraction is determined by the parameters f1 and f2, which indicate the fraction f1 of the smallest elements and the fraction f2 of the largest elements to be removed.
  • TrimmedMean[list,{f1,f2}] gives the mean of Sort[list,Less]〚1+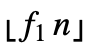;;n-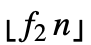〛, where n equals the length of list.
  • TrimmedMean[{{x1,y1,…},{x2,y2,…},…},f] gives {TrimmedMean[{x1,x2,…},f],TrimmedMean[{y1,y2,…},f],…}.
  • TrimmedMean[dist,{f1,f2}] gives Mean[TruncatedDistribution[Quantile[dist,{f1,1-f2}],dist]] for a univariate distribution dist.

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Trimmed mean after removing extreme values:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-cacnen
Out[1]=1

Trimmed mean after removing the smallest extreme values:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-clbc5x
Out[1]=1

Trimmed mean of a list of dates:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-prok5d
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-ziof1v
Out[2]=2

Trimmed mean of a symbolic distribution:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-b133z2
Out[1]=1

Scope  (10)Survey of the scope of standard use cases

Data  (9)

Exact input yields exact output:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-ug7y2
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-bcry2t
Out[2]=2

Approximate input yields approximate output:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-ksx55
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-d02ofx
Out[2]=2

TrimmedMean for a matrix gives columnwise means:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-jywoa6
Out[1]=1

Trimmed mean works with large arrays:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-enve04
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-if5yx4
Out[2]=2

SparseArray data can be used just like dense arrays:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-2bvdh
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-paeyu
Out[2]=2

Trimmed mean of a TimeSeries:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-tg8p6z
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-ffhpdi
Out[2]=2

Trimmed mean depends only on the values:

In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-fy9fte
Out[3]=3

Trimmed mean works with data involving quantities:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-jopin9
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-e8c21s
Out[2]=2

Compute trimmed mean of dates:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-b1smxx
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-pa4nmn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-uok1il
Out[3]=3

Compute trimmed mean of times:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-et9bla
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-ztsexm
Out[2]=2

List of times with different time zone specifications:

In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-mrqghz
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-ow7hca
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/05fh8k165m-rq9534
Out[5]=5

Distributions  (1)

The trimmed mean for a univariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-larmd5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-rxz55
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-eiu3ke
Out[3]=3

Applications  (3)Sample problems that can be solved with this function

Obtain a robust estimate of location when outliers are present:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-cexxtn
Out[1]=1

Extreme values have a large influence on the Mean:

In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-blrzc0
Out[2]=2

Simulate a trajectory with heavy-tailed measurement noise:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-f63fz9

The underlying signal and simulated path with noise:

In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-fh1mi1
Out[2]=2

Smooth the trajectory using a moving TrimmedMean:

In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-l6h0g9
In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-brc3ht

Increasing the block size gives a smoother trajectory:

In[5]:=5
✖
https://wolfram.com/xid/05fh8k165m-bb2lqb
Out[5]=5

Find a trimmed mean for the heights of children in a class:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-cevfij
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-fllmtw
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-celepo
Out[3]=3

Compare a few trimmed means:

In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-fgqfgk
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/05fh8k165m-cny2bx
Out[5]=5

Plot the trimmed mean as a function of trimmed fraction:

In[6]:=6
✖
https://wolfram.com/xid/05fh8k165m-dcgq58
In[7]:=7
✖
https://wolfram.com/xid/05fh8k165m-doz2wp
Out[7]=7

Properties & Relations  (5)Properties of the function, and connections to other functions

A 0% TrimmedMean is equivalent to Mean:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-k3hcsh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-fc96q6
Out[2]=2

TrimmedMean approaches Median as f approaches 1/2:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-dy2d21
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-h9emyc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-ed6bml
Out[3]=3

TrimmedMean of a distribution is the mean of its TruncatedDistribution:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-yd3d3n
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-lr5uh3
Out[2]=2

Mean of the TruncatedDistribution with appropriate bounds:

In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-clxbr6
In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-u4mwsn
Out[4]=4

TrimmedMean of a sample gives an estimate of the mean of a truncated distribution:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-jcz7or
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-dmr8h
Out[2]=2

Mean of the TruncatedDistribution with appropriate bounds:

In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-j8hhnt
In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-bo98xv
Out[4]=4

TrimmedMean drops the data beyond a certain quantile level, then computes the sample mean:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-cm3s6i
In[2]:=2
✖
https://wolfram.com/xid/05fh8k165m-01haem
In[3]:=3
✖
https://wolfram.com/xid/05fh8k165m-bgojw
Out[3]=3

WinsorizedMean clips the data beyond a certain quantile level, then computes the sample mean:

In[4]:=4
✖
https://wolfram.com/xid/05fh8k165m-wlch5r
In[5]:=5
✖
https://wolfram.com/xid/05fh8k165m-xbwg2
Out[5]=5

Plot the sorted data against the sample with elements removed and the clipped sample:

In[6]:=6
✖
https://wolfram.com/xid/05fh8k165m-gc5h1e
In[7]:=7
✖
https://wolfram.com/xid/05fh8k165m-elvj1j
Out[7]=7

Possible Issues  (1)Common pitfalls and unexpected behavior

TrimmedMean requires numeric values:

In[1]:=1
✖
https://wolfram.com/xid/05fh8k165m-g88
Out[1]=1
Wolfram Research (2007), TrimmedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/TrimmedMean.html (updated 2024).
✖
Wolfram Research (2007), TrimmedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/TrimmedMean.html (updated 2024).

Text

Wolfram Research (2007), TrimmedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/TrimmedMean.html (updated 2024).

✖
Wolfram Research (2007), TrimmedMean, Wolfram Language function, https://reference.wolfram.com/language/ref/TrimmedMean.html (updated 2024).

CMS

Wolfram Language. 2007. "TrimmedMean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TrimmedMean.html.

✖
Wolfram Language. 2007. "TrimmedMean." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/TrimmedMean.html.

APA

Wolfram Language. (2007). TrimmedMean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TrimmedMean.html

✖
Wolfram Language. (2007). TrimmedMean. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TrimmedMean.html

BibTeX

@misc{reference.wolfram_2025_trimmedmean, author="Wolfram Research", title="{TrimmedMean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TrimmedMean.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_trimmedmean, author="Wolfram Research", title="{TrimmedMean}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/TrimmedMean.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_trimmedmean, organization={Wolfram Research}, title={TrimmedMean}, year={2024}, url={https://reference.wolfram.com/language/ref/TrimmedMean.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_trimmedmean, organization={Wolfram Research}, title={TrimmedMean}, year={2024}, url={https://reference.wolfram.com/language/ref/TrimmedMean.html}, note=[Accessed: 29-March-2025 ]}