MinLimit

MinLimit[f,xx^*]

给出最小极限 _xx^*f(x).

MinLimit[f,{x₁,…,x_n}]

给出嵌套最小极限 ⋯ f (x₁,…,x_n).

MinLimit[f,{x₁,…,x_n}{,…,}]

给出多变量最小极限f (x₁,…,x_n).

更多信息和选项

MinLimit 也被称之为下极限、最大下界、liminf、下限和内限.
MinLimit 计算极限的最大下界，并总是为实数值函数定义. 当不需要实际极限时，它经常被用于给出收敛条件和其他渐近属性.
通过使用字符 （输入为 mlim 或 \[MinLimit]）带有上下标的最小极限可以按下输入：

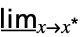	f	默认方向的最小极限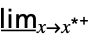
	f	上限的最小极限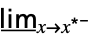
	f	下限的最小极限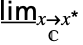
	f	复平面的最小极限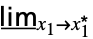
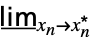	…f	MinLimit[f,{x₁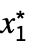,…,x_n}]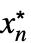

对于有限极限点 x^* 和 {,…,}：
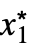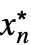MinLimit[f,xx^*]f^* $TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*$

MinLimit[f,{x₁,…,x_n}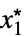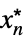{,…,}]f^* $TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*$
对于单变量 f[x]，定义使用最小包络 min[ϵ]MinValue[{f[x],0< $TemplateBox[{{x, -, {x, ^, *}}}, Abs]$ <ϵ},x]，对于多变量 f[x₁,…,x_n]，min[ϵ]MinValue[{f[x₁,…,x_n],0< $TemplateBox[{{{, {{{x, _, {(, 1, )}}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]$ <ϵ},{x₁,…,x_n}]. 当 ϵ0，函数 min[ϵ] 单调增加，因此总是有极限，可能是 ±∞.
下图用蓝色显示 min[ $TemplateBox[{{x, -, {x, ^, *}}}, Abs]$ ] 和 min[].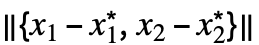

对于无穷极点 x^*∞，最小包络 min[ω]MinValue[{f[x],x>ω},x] 用于单变量 f[x]，min[ω]MinValue[{f[x₁,…,x_n],x₁>ω∧⋯∧x_n>ω},{x₁,…,x_n}] 用于多变量 f[x₁,…,x_n]. 函数 min[ω] 当 ω∞ 时，单调递增，因此总有极限.
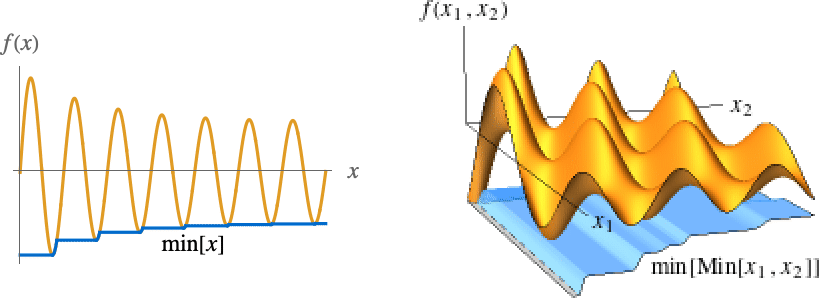
下图用蓝色显示 min[x] 和 min[Min[x₁,x₂]].

如果找不到最小极限，MinLimit 返回未被计算的.
可以给出以下选项：

Assumptions	$Assumptions	参数的假设
Direction	Reals	接近极限点的方向
GenerateConditions	Automatic	是否产生参数条件
Method	Automatic	使用的方法
PerformanceGoal	"Quality"	性能方面的优化

Direction 的可能设置包括：

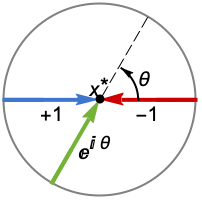
	Reals 或 "TwoSided"	来自于两个实数域方向
	"FromAbove" or -1	来自于上限或更大的值
	"FromBelow" or +1	来自于下限或更小的值
	Complexes	来自于所有复数方向
	Exp[ θ]	方向为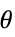
	{dir₁,…,dir_n}	对变量 x_i 分别使用方向 dir_i

在 x^* 的 DirectionExp[ θ] 表明接近极限点 x^* 的曲线的方向切线.

GenerateConditions 的可能设置包括：
Automatic 只是非通用条件

True 所有条件

False 无条件

None 如果需要条件则返回未被计算的
PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 设置为 "Quality"， MinLimit 一般能解决更多问题或产生更简单的结果，但潜在使用更多的时间和内存.

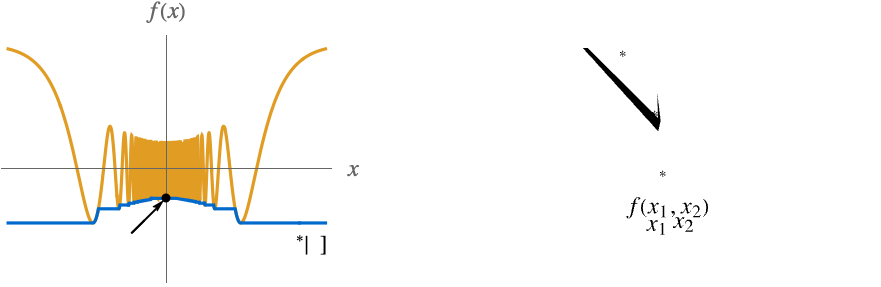
范例

打开所有单元关闭所有单元

基本范例 (3)

在无穷处的最小极限：

函数会越来越接近，但不会接触到 -1：

无穷最小极限：

接近不连续，会有任意小的值：

距上限的最小极限：

距下限的最小极限：

两边的最小极限是其中更小的那个：

范围 (35)

基本用途 (5)

求点上的最小极限：

求符号点上的最小极限：

求 -Infinity 上的最小极限：

当，然后的嵌套最小极限：

当，计算多变量最小极限：

排版极限 (4)

使用 mlim 输入  字符，键入创建下标：

通过在极限点上使用上标或获取上限或下限的极限：

输入零后，使用创建上标：

为了指定 Reals 或 Complexes 的方向，在  字符的下标中输入域：

输入规则 ->，使用创建下标，敲入 reals 以便输入：

TraditionalForm 格式化：

基础函数 (10)

多项式：

奇点的有理函数：

在 ±Infinity 上的有理函数：

代数函数：

奇点的三角函数：

±Infinity 上的三角函数：

逆三角函数：

指数函数：

当，函数衰减比任何的幂都快：

相反，比的任何幂都快，但乘积的符号取决于的奇偶性：

可视化表示函数：

对数函数：

分段函数 (5)

非连续的分段函数：

左连续的分段函数：

两边的最小极限是其中最小的那个：

UnitStep 是有效的右连续分段函数：

RealSign 是有效的非连续分段函数：

注意，与任何值无关：

当 x 趋近整数值，求 Floor 的最小极限：

特殊函数 (4)

涉及 Gamma 的最小极限：

涉及贝塞尔类型的函数的最小极限：

涉及指数积分的最小极限：

在每个非正的偶整数，Gamma 从一边发散到：

嵌套的最小极限 (3)

当，然后，计算嵌套的的最小极限：

通过计算两个 MinLimit 表达式获取同样的结果：

当，然后计算最小极限会产生不同的答案：

这个等于两个嵌套的最小极限：

当，然后，嵌套的最小极限是：

当，然后，嵌套的最小极限为：

考虑原点两个变量的函数：

当，然后的迭代最小极限为：

当在几乎取消给出任意小的值，真双变量最小极限为：

比如，该值可以沿着曲线趋近：

沿着先前计算的两轴可视化函数和值：

多变量最小极限 (4)

求多变量函数的最小极限：

两个嵌套最小极限给出不同的答案：

沿着曲线接近原点产生第三种结果：

函数的真二维下限是，沿着轴获取：

可视化原点附近的最小和最大值：

求双变量函数的最小极限：

函数的真二维最小极限为：

注意，迭代极限并没有给出结果：

确实，沿着任何斜率，函数是常数：

当接近，沿着曲线接近最小，例如 :

可视化函数和三个计算的最小极限：

求在原点双变量函数的最小极限：

在原点真二维最小极限是 :

用极坐标重新表示函数：

极坐标表达式是有界的并且当消失，剩下 Sin 的最小极限：

计算三变量函数的最小极限：

在原点的最小极限是：

注意，各种迭代的最小极限为 0：

这是因为最小值是沿着线、获取：

通过转换成球坐标可以理解最小极限：

可视化函数：

选项 (10)

Assumptions (1)

使用 Assumptions 指定参数上的条件：

不同假设会产生不同的结果：

Direction (5)

下限的最小极限：

等同于：

上限的最小极限：

等同于：

默认方向是 Reals：

"TwoSided" 等同于 Reals：

复平面上的最小极限：

在实域上比较极限：

分支切割处的最小极限：

计算从不同象限趋近的二元最小极限：

从第一象限趋近原点：

等同于：

从第二象限趋近原点：

从左半平面趋近原点：

从底半平面趋近原点：

可视化函数：

GenerateConditions (3)

返回没有条件说明的结果：

只有当 n>0，结果才有效：

如果结果依赖于参数值返回未被计算的：

默认情况下，返回唯一结果的会产生条件：

默认情况下，如果特殊值使得结果无效，则不会产生条件：

当 GenerateConditions->True，也会报告这些非普通的条件：

PerformanceGoal (1)

使用 PerformanceGoal 避免潜在的昂贵计算：

默认设置使用所有可能技术来尝试产生结果：

应用 (12)

最小极限的几何 (3)

在，函数有最小极限：

这意味着必须有一序列，其中，当，；例如，:

数值上，时，很快：

确切计算两个序列极限：

注意，该序列极限存在，甚至当时，本身没有极限：

当趋近，函数有极限 0：

因此，它的最小极限为 0：

在周围递增地小区域，平坦增加，大部分图是在之下：

当趋近，函数没有极限：

然而，它的最小极限是：

在周围递增地小区域，反弹很大，但慢慢成为其边界：

渐进分析 (2)

在 a，函数是 "big-o of "，写作，如果 $_(x->_(TemplateBox[{}, Reals])a)TemplateBox[{{{(, {f, (, x, )}, )}, /, {(, {g, (, x, )}, )}}}, Abs]>0$ ：

比如，是：

但不是：

陈述总是为真：

如果并且，那么：

有可能函数并没有共享任何关系：

因此，函数的自反部分阶：

如果没有那么快趋近 0：

求关键驱动的质点弹簧系统的运动：

运动是振荡的，但是变成任意为负，表示不稳定性：

添加过阻尼系统：

振荡运动是有界的，并且最终受限于，表示稳定性：

连续性 (4)

如果，则函数在处下半连续. SawtoothWave 在处下半连续：

可视化函数：

另一方面，RealSign 在原点处不下半连续：

可视化函数：

考虑下面的函数：

该函数在原点处下半连续：

尽管 f 在原点处没有左右极限：

注意，f 的 MinLimit 不依赖于 f 在零处的值，因此，任何小于的值都将使 f 下半连续：

可视化 f：

如果，则函数在处上半连续. 当且仅当实值函数同时上半连续和下半连续，函数才是连续的. UnitStep 在处上半连续：

但是，它不是下半连续的，因此在原点处不连续：

另一方面，下式显示 TriangleWave 在原点处连续：

可视化这两个函数：

Ceiling 是不连续的，但是在每个整数处下半连续：

另一方面，Floor 在整数处既不连续，也不是下半连续的：

两者在非整数值处都是连续的，但只要 Ceiling 在所有的上是下半连续的：

微分 (3)

左下 Dini 导数被定义为：

右下 Dini 导数也被类似定义：

在整条实数线上，Ramp 具有有限下 Dini 导数：

注意，这两个导数是处处相等的除了原点：

这也反应了这个事实，Ramp 是处处可微，除了原点：

考虑以下函数：

在原点连续：

但是，它既没有左导数也没有右导数：

然而，它有有限 Dini 导数：

这表明零点附近函数的增长是有界的：

有两个左 Dini 导数. 第一个是左下 Dini 导数，定义如下：

右下 Dini 导数使用最大极限进行类似定义：

在处右可导，当且仅当这两个是等价的和有限的，正如 Ramp 在的情况：

然而，函数在原点没有左导数：

属性和关系 (13)

实值函数总是有（可能无穷）最小极限：

对应的极限可能不存在：

正的乘法常数可移至最小极限的外面：

如果当，和有有限的最小极限，那么：

在这种情况下，有严格的不等性：

Assumptions 可用于最小极限表达式的参数：

Direction 在极限变量上放置条件：

当计算嵌套的最小极限时，会对后面的极限变量产生适当的假设：

比较：

对于实值函数，如果存在 Limit，那么 MinLimit 具有同样的值：

如果当，有有限极限，那么：

MinLimit 总是小于或等于 MaxLimit:

如果 MaxLimit 等于 MinLimit，那么存在极限并等于它们的共同的值：

如果最小极限是，那么最大极限，极限也是 :

MinLimit 可以被计算为 -MaxLimit[-f,…]：

如果对于，，那么：

如果两个最小极限相等——比如这个例子——那么，当， f 有极限：

这是 "squeezing" 或 "sandwich" 理论的生成：

MinLimit 总是小于等于 DiscreteMinLimit：

可能存在的问题 (1)

MinLimit 只为实值函数定义：

巧妙范例 (1)

可视化一套最小极限：

顶部

	MinLimit[f,xx^]f^	$TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*$
	MinLimit[f,{x₁,…,x_n}{,…,}]f^*	$TemplateBox[{{min, (, epsilon, )}, epsilon, 0, +, {Direction, ->, {-, 1}}}, LimitWithSuperscript, DisplayFunction -> ({Sequence[{Sequence["lim"], _, DocumentationBuild`Utils`Private`Parenth[{#2, ->, {#3, ^, DocumentationBuild`Utils`Private`Parenth[#4]}}, LimitsPositioning -> True]}], #1} & ), InterpretationFunction -> ({Limit, [, {#1, ,, {#2, ->, #3}, ,, #5}, ]} & )]=f^*$

	Automatic	只是非通用条件
	True	所有条件
	False	无条件
	None	如果需要条件则返回未被计算的

MinLimit

更多信息和选项

范例

基本范例 (3)

范围 (35)

基本用途 (5)

排版极限 (4)

基础函数 (10)

分段函数 (5)

特殊函数 (4)

嵌套的最小极限 (3)

多变量最小极限 (4)

选项 (10)

Assumptions (1)

Direction (5)

GenerateConditions (3)

PerformanceGoal (1)

应用 (12)

最小极限的几何 (3)

渐进分析 (2)

连续性 (4)

微分 (3)

属性和关系 (13)

可能存在的问题 (1)

巧妙范例 (1)

参见

相关指南

历史

文本

CMS

APA

BibTeX

BibLaTeX