RealSign

RealSign[x]

gives -1, 0 or 1 depending on whether x is negative, zero or positive.

Details

  • RealSign is also known as sgn or signum.
  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • RealSign[x] is equivalent to Piecewise[{{-1,x<0},{1,x>0}}].
  • RealSign is piecewise constant and differentiable everywhere except at the origin.
  • RealSign tries various transformations in trying to determine the sign of symbolic expressions.
  • For exact numeric quantities, RealSign internally uses numerical approximations to establish its result. This process can be affected by the setting of the global variable $MaxExtraPrecision.
  • RealSign automatically threads over lists. »
  • RealSign can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (4)

Positive numbers:

Negative numbers:

Plot RealSign over a subset of the reals:

Derivative of RealSign:

Indefinite integral:

Scope  (28)

Numerical Evaluation  (5)

Evaluate numerically:

RealSign remains unevaluated for imaginary numbers:

RealSign always returns an infinite-precision result:

Compute the elementwise values of an array using automatic threading:

Or compute the matrix RealSign function using MatrixFunction:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Specific Values  (5)

Values of RealSign at fixed points:

Value at zero:

Values at infinity:

Evaluate symbolically:

Find a value of for which the TemplateBox[{x}, RealSign]=0:

Visualize the result:

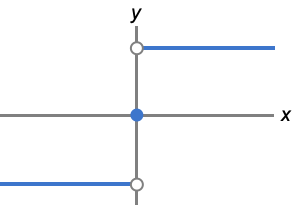
Visualization  (3)

Plot TemplateBox[{{1, +, x}}, RealSign]:

Plot RealSign along with its first derivative:

Plot RealSign in three dimensions:

Function Properties  (10)

RealSign is only defined for real inputs:

Function range of RealSign:

RealSign is an odd function:

RealSign is not an analytic function:

It has both a singularity and a discontinuity:

RealSign is nondecreasing:

RealSign is not injective:

RealSign is not surjective:

RealSign is neither non-negative nor non-positive:

RealSign is neither convex nor concave:

TraditionalForm formatting:

Differentiation and Integration  (5)

First derivative with respect to :

Obtain an equivalent expression using the definition of derivative:

The function Sign of complex variables is not differentiable:

Its higher derivatives are equal to its first derivative:

Compute the indefinite integral using Integrate:

Definite integral:

More integrals:

Applications  (6)

Solve a differential equation with RealSign:

Compute the Fourier cosine series of RealSign:

Solve an equation involving RealSign:

Prove an inequality containing RealSign:

Simplify expressions containing RealSign:

Define Rademacher functions:

Plot (vertically shifted) Rademacher functions:

Check orthogonality over the unit interval:

Properties & Relations  (9)

RealSign is defined only for real numbers:

Sign is defined for complex numbers:

RealSign is a differentiable function:

Sign is not differentiable:

RealSign is an integrable function:

Sign is integrable only for real arguments:

RealSign is idempotent:

Use FullSimplify to simplify expressions involving RealSign:

Definite integration:

Integral transforms:

Convert into Piecewise:

Denest:

Possible Issues  (4)

For purely real arguments, RealSign returns exact answers:

RealSign can stay unevaluated for numeric arguments:

Use Simplify to obtain the sign of the expression:

Machine‐precision numerical evaluation of RealSign can give wrong results:

Arbitrary‐precision evaluation gives the correct result:

A larger setting for $MaxExtraPrecision can be necessary:

RealSign applied to a matrix does not give the matrix sign function:

Neat Examples  (3)

Form repeated convolution integrals starting with a symmetric product of three sign functions:

Approximate RealSign through a generalized Fourier series:

Calculate rational approximations of RealSign:

Wolfram Research (2017), RealSign, Wolfram Language function, https://reference.wolfram.com/language/ref/RealSign.html (updated 2021).

Text

Wolfram Research (2017), RealSign, Wolfram Language function, https://reference.wolfram.com/language/ref/RealSign.html (updated 2021).

CMS

Wolfram Language. 2017. "RealSign." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/RealSign.html.

APA

Wolfram Language. (2017). RealSign. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RealSign.html

BibTeX

@misc{reference.wolfram_2025_realsign, author="Wolfram Research", title="{RealSign}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/RealSign.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_realsign, organization={Wolfram Research}, title={RealSign}, year={2021}, url={https://reference.wolfram.com/language/ref/RealSign.html}, note=[Accessed: 22-February-2025 ]}