NeymanScottPointProcess

NeymanScottPointProcess[μ,λ,rdist,d]

における，密度関数 μ，クラスタ平均 λ，放射状クラスタ点分布 rdist のネイマン(Neyman)・スコット(Scott)点過程を表す．

NeymanScottPointProcess[μ,λ,mdist,d]

において多変量クラスタ点分布 mdist を使う．

詳細

  • NeymanScottPointProcessは中心衛星過程としても知られている．
  • NeymanScottPointProcessは，非同次ポアソン(Poisson)点過程に従って配置された中心と，クラスタ分布に従って中心の周りに分布されたクラスタ点を使用して，クラスタ化された点配置をモデル化する．
  • 主に，野生動物の群れ，親木の周りの苗のクラスタ，爆撃パターン，昆虫の幼虫のパターンのモデリングに使われる．
  • クラスタの中心は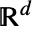，内で密度関数 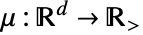のInhomogeneousPoissonPointProcessに従って置かれる．
  • クラスタの点の数は平均 λ のPoissonDistributionに従って分布する．
  • 等方性分布に従うクラスタ点は動径分布 rdist を使って最も簡単に指定できる．
  • 一般的なクラスタ分布は多変量分布 mdist を使って指定できる．
  • NeymanScottPointProcessは一般的なポアソンクラスタ過程である．一般的なポアソンクラスタ過程にはそれぞれ専用の関数があり，該当する場合はより簡単かつ効率的に使うことができる．
  • 過程動径分布特徴
    MaternPointProcess一様クラスタ点
    ThomasPointProcess法線クラスタ点
    CauchyPointProcess裾の重いクラスタ点
    VarianceGammaPointProcess法線ガンマ混合クラスタ点
  • NeymanScottPointProcessでは，λ は任意の正の実数でよく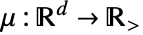，で，d は任意の正の整数でよい．
  • PointProcessEstimatorでNeymanScottPointProcessを推定するために次の設定を使うことができる．
  • "FindClusters"FindClusters関数を使う
    "MethodOfMoments"一様測度を使ってパラメータを推定する
  • NeymanScottPointProcessは，RipleyK，PointCountDistribution，RandomPointConfiguration等の関数と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (4)

放射クラスタ分布に従うネイマン・スコット点過程からサンプルを取る：

多変量クラスタ分布に従う単位球上の3Dネイマン・スコット点過程からサンプルを取る：

地理領域からサンプルを取る：

有効な密度関数はInhomogeneousPoissonPointProcessについてと同じである：

スコープ  (2)

次元が埋込み次元に等しい有効な領域からサンプルを取る：

領域内のネイマン・スコット点過程からサンプルを取り，点を可視化する：

ネイマン・スコット点過程からの点配置のシミュレーションを行う：

"FindClusters"法を使って点過程モデルを推定する：

特性と関係  (1)

PointCountDistributionは既知である：

平均と分散：

確率密度関数をプロットする：

分布のシミュレーションを行う：

確率密度ヒストグラム：

Wolfram Research (2020), NeymanScottPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.

テキスト

Wolfram Research (2020), NeymanScottPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.

CMS

Wolfram Language. 2020. "NeymanScottPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.

APA

Wolfram Language. (2020). NeymanScottPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html

BibTeX

@misc{reference.wolfram_2024_neymanscottpointprocess, author="Wolfram Research", title="{NeymanScottPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_neymanscottpointprocess, organization={Wolfram Research}, title={NeymanScottPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html}, note=[Accessed: 18-November-2024 ]}