CauchyPointProcess[μ,λ,b,d]
represents a Cauchy cluster point process with density μ, cluster mean λ and scale parameter b in ![]() .
.


CauchyPointProcess
CauchyPointProcess[μ,λ,b,d]
represents a Cauchy cluster point process with density μ, cluster mean λ and scale parameter b in ![]() .
.
Details


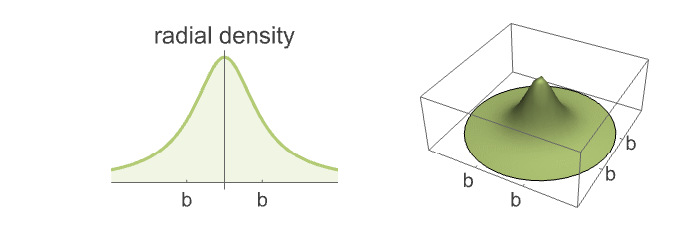
- CauchyPointProcess models clustered point configurations with centers uniformly distributed over space and cluster points isotropically distributed with a heavy-tail radial distribution.
- Typical uses include forestry to model locations of trees such as long-leaf pines, where the seeds can occasionally be dispersed a long distance from their source.
- The cluster centers are placed according to PoissonPointProcess with density μ.
- The point count of a cluster is distributed according to PoissonDistribution with mean λ.
- The cluster points in each cluster in
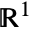 are distributed according to CauchyDistribution[0,b].
are distributed according to CauchyDistribution[0,b]. - The cluster points in
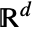 are distributed according to MultivariateTDistribution[DiagonalMatrix[{b2,b2,…}],1] centered at a cluster center.
are distributed according to MultivariateTDistribution[DiagonalMatrix[{b2,b2,…}],1] centered at a cluster center. - CauchyPointProcess allows μ, λ and b to be any positive real numbers, and d to be any positive integer.
- The following settings can be used for PointProcessEstimator for estimating CauchyPointProcess:
-
"FindClusters" use FindClusters function "MethodOfMoments" use a homogeneity measure to estimate the parameters - CauchyPointProcess can be used with such functions as RipleyK, PointCountDistribution and RandomPointConfiguration.

Examples
open all close allBasic Examples (3)
Scope (3)
Sample from a valid region whose dimension is equal to its embedding dimension:
Sample from a Cauchy point process in the region and visualize the points:
Use the "FindClusters" method to estimate a point process model:
Compare the Ripley ![]() measure between the original process and the estimated model:
measure between the original process and the estimated model:
Properties & Relations (6)
PointCountDistribution is known:
The probability density histogram:
Ripley's ![]() and Besag's
and Besag's ![]() for Cauchy point process in 2D:
for Cauchy point process in 2D:
Ripley's ![]() of a Cauchy point process is larger than for a Poisson point process:
of a Cauchy point process is larger than for a Poisson point process:
Compare to the Poisson point process:
Besag's ![]() of a Cauchy point process is larger than for a Poisson point process:
of a Cauchy point process is larger than for a Poisson point process:
Compare to the Poisson point process:
Pair correlation of a Cauchy point process is larger than 1:
Related Guides
History
Text
Wolfram Research (2020), CauchyPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/CauchyPointProcess.html.
CMS
Wolfram Language. 2020. "CauchyPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CauchyPointProcess.html.
APA
Wolfram Language. (2020). CauchyPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CauchyPointProcess.html
BibTeX
@misc{reference.wolfram_2025_cauchypointprocess, author="Wolfram Research", title="{CauchyPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/CauchyPointProcess.html}", note=[Accessed: 20-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_cauchypointprocess, organization={Wolfram Research}, title={CauchyPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/CauchyPointProcess.html}, note=[Accessed: 20-January-2026]}