NeymanScottPointProcess
NeymanScottPointProcess[μ,λ,rdist,d]
表示一个 Neyman–Scott 点过程,其密度函数为 μ,聚类均值为 λ,在 ![]() 中的径向聚类点分布为 rdist.
中的径向聚类点分布为 rdist.
NeymanScottPointProcess[μ,λ,mdist,d]
使用 ![]() 中的多变量聚类点分布 mdist.
中的多变量聚类点分布 mdist.
更多信息


- NeymanScottPointProcess 亦称为中心-卫星过程.
- NeymanScottPointProcess 模拟聚类点布局,其中心按非齐次泊松点过程放置,聚类点在中心周围的分布服从聚类分布.
- 典型用途包括野生动物群、亲本树周围的幼苗簇、模拟轰炸模式和昆虫幼虫模式.
- 根据 InhomogeneousPoissonPointProcess 放置聚类中心,在
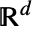 中,其密度函数为
中,其密度函数为 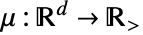 .
. - 聚类的点数则按均值为 λ 的 PoissonDistribution 分布.
- 可使用径向分布 rdist 很容易地指定遵循各向同性分布的聚类点.
-

- 可以使用多变量分布 mdist 指定一般聚类分布.
-

- NeymanScottPointProcess 是一般的泊松聚类过程;有专门的函数描述常见的泊松聚类过程,并且在适用情况下更易于使用且效率更高.
-
过程 径向分布 特性 MaternPointProcess 
均匀的聚类点 ThomasPointProcess 
正态聚类点 CauchyPointProcess 
重尾聚类点 VarianceGammaPointProcess 
正态和伽玛混合的聚类点 - NeymanScottPointProcess 允许 λ 为任意正实数,
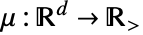 ,允许 d 为任意正整数.
,允许 d 为任意正整数. - PointProcessEstimator 可使用以下设置来估计 NeymanScottPointProcess:
-
"FindClusters" 使用 FindClusters 函数 "MethodOfMoments" 使用同质性度量来估计参数 - NeymanScottPointProcess 可与诸如 RipleyK、PointCountDistribution 和 RandomPointConfiguration 这样的函数一起使用.
范例
打开所有单元关闭所有单元基本范例 (4)
来自服从径向聚类分布的 Neyman–Scott 点过程的样本:
来自单位球体上服从多变量聚类分布的 3D Neyman–Scott 点过程的样本:
有效密度函数与 InhomogeneousPoissonPointProcess 相同:
范围 (2)
属性和关系 (1)
Wolfram Research (2020),NeymanScottPointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.
文本
Wolfram Research (2020),NeymanScottPointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.
CMS
Wolfram 语言. 2020. "NeymanScottPointProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html.
APA
Wolfram 语言. (2020). NeymanScottPointProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NeymanScottPointProcess.html 年