Xor

Xor[e1,e2,…]

is the logical XOR (exclusive OR) function. It gives True if an odd number of the e_(i) are True, and the rest are False. It gives False if an even number of the e_(i) are True, and the rest are False.

Details

  • Xor[e1,e2,…] can be input in StandardForm and InputForm as 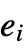e_(1) xor e_(2) xor .... The character ⊻ can be entered as 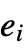xor or \[Xor].
  • Xor gives symbolic results when necessary, applying various simplification rules to them.
  • Unlike And, Nand, Or, and Nor, Xor must always test all its arguments, and so is not a control structure, and does not have attribute HoldAll.

Examples

open allclose all

Basic Examples  (2)

Enter using xor:

Scope  (4)

Xor is associative and commutative:

Do symbolic simplification:

Expand in terms of And, Or, and Not:

TraditionalForm formatting:

Applications  (3)

Find the Xor of two regions in 2D:

Find the Xor of three regions in 3D:

A cellular automaton based on Xor:

Find the area of the symmetric difference of sets given by algebraic conditions:

This shows the set:

Properties & Relations  (3)

Truth table for binary Xor:

Ternary Xor:

Use BooleanConvert to expand in terms of And, Or, and Not:

Xor of conditions in Boole functions:

Neat Examples  (2)

The Xor of disks on a circle:

Generate three disks on a circle:

A truth table for a 12-variable Xor function:

Wolfram Research (1988), Xor, Wolfram Language function, https://reference.wolfram.com/language/ref/Xor.html (updated 2003).

Text

Wolfram Research (1988), Xor, Wolfram Language function, https://reference.wolfram.com/language/ref/Xor.html (updated 2003).

CMS

Wolfram Language. 1988. "Xor." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2003. https://reference.wolfram.com/language/ref/Xor.html.

APA

Wolfram Language. (1988). Xor. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Xor.html

BibTeX

@misc{reference.wolfram_2024_xor, author="Wolfram Research", title="{Xor}", year="2003", howpublished="\url{https://reference.wolfram.com/language/ref/Xor.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_xor, organization={Wolfram Research}, title={Xor}, year={2003}, url={https://reference.wolfram.com/language/ref/Xor.html}, note=[Accessed: 22-November-2024 ]}