ParameterMixtureDistribution

ParameterMixtureDistribution[dist[θ],θwdist]

母数 θ が重み分布 wdist に従って分布する母数混合分布を表す．

ParameterMixtureDistribution[dist[θ1,θ2,…],{θ1wdist1,θ2wdist2,…}]

母数 θ1が重み分布 wdist1に，母数 θ2が重み分布 wdist2にというように順に従う母数混合分布を表す．

詳細とオプション

  • 値 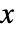の確率密度はExpectation[PDF[dist[θ],x],θwdist]で与えられる．
  • 重み分布 wdist の領域は dist[θ]で期待される母数領域と等しいかその部分集合でなければならない．
  • 母数 θiは離散的でも連続的でもよい．
  • 母数についての仮定は，Assumptionsassum を使って指定することができる．
  • ParameterMixtureDistributionはMean，CDF，RandomVariate等の関数で使うことができる．

例題

すべて開くすべて閉じる

例  (3)

母数混合分布を指定する：

母数混合分布は他の任意の分布と同じように動作する：

多変量分布の母数混合分布を求める：

スコープ  (36)

基本的な用法  (7)

一様分布に従う重みのExponentialDistributionの母数混合分布を求める：

確率密度関数：

重み領域は主分布の母数推定を満足しなければならない：

正の実数についてサポートされている重み分布を取り上げる：

結果として得られる母数混合分布の累積分布関数：

離散母数に離散的な重みを使用する：

確率密度関数を比較する：

各分布から4より小さい値を得る確率を比較する：

1つの母数のみを変える：

累積分布関数：

平均と分散：

多変量分布を重みとして使って2つ以上の母数を変える：

2つ以上の重み分布を使って複数の母数を変える：

確率密度関数を可視化する：

母数混合分布の母数を推定する：

重み分布母数の選択用にランダムサンプルを作成する：

分布母数を求める：

サンプルのヒストグラムを推定分布の確率密度関数と比較する：

重み分布  (5)

一変量連続重み分布の母数混合分布を定義する：

一変量離散重み分布の母数混合分布を定義する：

確率密度関数を求める：

Momentは記号次数については閉形式である：

一変量離散重み分布の母数混合分布を定義する：

確率密度関数：

多変量重み分布の母数混合分布を定義する：

確率密度関数：

確率密度関数の積分が1であることを証明する：

2つ以上の重み分布を使う：

平均：

分散：

パラメトリック分布  (8)

一変量連続分布の母数混合分布を定義する：

累積分布関数：

一変量連続分布の混合分布を求める：

確率密度関数：

一変量離散分布の母数混合分布を定義する：

ランダムサンプルを生成する：

平均と分散を求める：

一変量離散分布の母数混合分布を求める：

確率密度関数：

平均と分散：

の固定した値について，Momentは記号次数の下では閉形式である：

二変量連続分布の母数混合分布を定義する：

ランダムサンプルと平滑化されたヒストグラムを使って密度関数を可視化する：

二変量分布の母数混合分布を定義する：

確率密度関数：

平均：

共分散行列：

多変量離散分布の母数混合分布を求める：

ランダムサンプルを生成する：

各成分のヒストグラム：

LaplaceDistributionは母数混合分布として表すことができる：

ノンパラメトリック分布  (3)

EmpiricalDistributionを重みとして使う：

確率密度関数：

HistogramDistributionを重みとして使う：

確率密度関数：

SmoothKernelDistributionを重みとし，母数混合分布を定義する：

確率密度関数をプロットする：

累積分布関数をプロットする：

派生分布  (11)

ProductDistributionを母数混合分布中の重み分布として使う：

からのランダムサンプルのヒストグラムを使って確率密度関数を可視化する：

TransformedDistributionの母数混合分布を求める：

ランダムサンプルを使って密度関数を可視化する：

TransformedDistributionを重み分布として使って母数混合分布を求める：

確率密度関数：

MixtureDistributionを母数混合分布で重み分布として使う：

確率密度関数：

平均と分散：

確率分布に従ってMixtureDistribution中の重みを変化させる：

確率密度関数：

平均値での固定した重みのMixtureDistributionと比較する：

両方の密度関数は等しい：

TruncatedDistributionの母数混合分布を定義する：

平均と分散：

TruncatedDistributionの母数分布を定義する：

ランダムサンプルを使って確率密度関数を可視化する：

母数混合分布でTruncatedDistributionを重み分布として使う：

確率密度関数：

平均：

OrderDistributionの母数混合分布を求める：

確率密度関数：

OrderDistributionを重み分布として使う：

確率密度関数：

QuantityDistributionの母数混合を評価するとQuantityDistributionになる：

自動簡約  (2)

離散分布  (1)

BetaDistributionを重みとした母数混合分布：

PoissonDistributionを含む母数混合分布：

連続分布  (1)

RayleighDistributionを含む母数混合分布：

NormalDistributionを含む母数混合分布：

オプション  (1)

Assumptions  (1)

WaringYuleDistributionは幾何分布とUniformDistributionの母数混合分布である：

組込みの答と比較する：

アプリケーション  (7)

SuzukiDistributionはRayleighDistributionとLogNormalDistributionの母数混合分布として定義される：

KDistributionはRayleighDistributionとGammaDistributionの母数混合分布として表すことができる：

銀行員が各顧客の応対に要する時間（単位：分）は，平均3のLindleyDistributionに従う平均時間 のExponentialDistributionに従う．応対時間の分布を求める：

確率密度関数：

平均応対時間：

次の30人の顧客に対する応対時間のシミュレーションを行う：

光通信システムでは，送信された光が受信器で電流を生成する．電子の数は光のタイプによってポアソン分布と他の分布の母数混合分布に従う．光源が強度 のコヒーレントレーザー光線を使う場合，電子数はポアソン分布に従う：

これはPoissonDistributionである：

光源が熱照明を使う場合，ポアソン母数は母数 でExponentialDistributionに従い，電子数の分布が決定できる：

これら2つの分布は弁別可能なので光源のタイプが識別できる：

Doppler(Cauchy)プロファイルとLorentzian（正規）プロファイルを組み合せた結果の，Voigtスペクトル線プロファイル：

密度関数を計算する：

密度関数をプロットする：

プロファイルの半値幅を計算する：

修正正規分布を定義する：

のいくつかの値について修正正規分布密度をプロットし，それらを標準正規分布密度と比較する：

多変量ポリヤ(Pólya)分布を定義する：

確率密度関数：

特性と関係  (4)

母数混合分布の確率密度関数はExpectationを使って計算できる：

有限数の値を仮定すると，離散重み分布を持つ母数混合分布はMixtureDistributionとして表すことができる：

確率密度関数を比較する：

数えられる数の値を仮定すると，離散重み分布を持つ母数混合分布はMixtureDistributionで近似することができる：

異なる分位点をカットオフとした近似を比較する：

連続重み分布を持つ母数混合分布をMixtureDistributionで近似する：

確率密度関数を比較する：

Wolfram Research (2010), ParameterMixtureDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), ParameterMixtureDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "ParameterMixtureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html.

APA

Wolfram Language. (2010). ParameterMixtureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html

BibTeX

@misc{reference.wolfram_2024_parametermixturedistribution, author="Wolfram Research", title="{ParameterMixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parametermixturedistribution, organization={Wolfram Research}, title={ParameterMixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}, note=[Accessed: 22-November-2024 ]}