BetaDistribution[α,β]
represents a continuous beta distribution with shape parameters α and β.


BetaDistribution
BetaDistribution[α,β]
represents a continuous beta distribution with shape parameters α and β.
Details
- The probability density for value
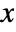 in a beta distribution is proportional to
in a beta distribution is proportional to 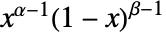 for
for  , and is zero for
, and is zero for 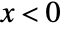 or
or 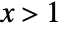 . »
. » - BetaDistribution allows α and β to be any positive real numbers.
- BetaDistribution allows α and β to be dimensionless quantities. »
- BetaDistribution can be used with such functions as Mean, CDF, and RandomVariate. »
Background & Context
- BetaDistribution[α,β] represents a statistical distribution defined over the interval
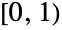 and parametrized by two positive values α, β known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of α and β, the PDF of the beta distribution may be monotonic increasing, monotonic decreasing, or unimodal with potential singularities approaching the boundaries of its domain.
and parametrized by two positive values α, β known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of α and β, the PDF of the beta distribution may be monotonic increasing, monotonic decreasing, or unimodal with potential singularities approaching the boundaries of its domain. - The beta distribution arises as a prior distribution for binomial proportions in Bayesian analysis. It is also commonly used to model random variables limited to a finite interval. For example, the distribution of the
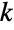
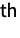 smallest element in a continuous, independent, and uniformly distributed sample of size of
smallest element in a continuous, independent, and uniformly distributed sample of size of 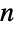 can be computed using OrderDistribution[{UniformDistribution[],n},k] and is precisely equal to BetaDistribution[k,n-k+1]. In addition to its statistical significance, the beta distribution also plays a fundamental role in a number of scientific fields, including phenomena related to allele frequency distribution, soil property variability, geological mineral-to-rock ratios, and HIV transmission behavior.
can be computed using OrderDistribution[{UniformDistribution[],n},k] and is precisely equal to BetaDistribution[k,n-k+1]. In addition to its statistical significance, the beta distribution also plays a fundamental role in a number of scientific fields, including phenomena related to allele frequency distribution, soil property variability, geological mineral-to-rock ratios, and HIV transmission behavior. - RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a beta distribution. Distributed[x,BetaDistribution[α,β]], written more concisely as xBetaDistribution[α,β], can be used to assert that a random variable x is distributed according to a beta distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BetaDistribution[α,β],x] and CDF[BetaDistribution[α,β],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a beta distribution, EstimatedDistribution to estimate a beta parametric distribution from given data, and FindDistributionParameters to fit data to a beta distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic beta distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic beta distribution.
- TransformedDistribution can be used to represent a transformed beta distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a beta distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving beta distributions.
- The beta distribution is related to a number of other distributions. For example, BetaDistribution is the so-called "conjugate prior" for the parameters of a number of other distributions, including BernoulliDistribution, BinomialDistribution, NegativeBinomialDistribution, and GeometricDistribution. Moreover, BetaDistribution generalizes both UniformDistribution and PowerDistribution in the sense that (modulo inclusion of the endpoints
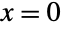 and
and 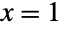 ), PDF[BetaDistribution[1,1],x] is equal to both PDF[UniformDistribution[],x] and PDF[PowerDistribution[1,1],x]. BetaDistribution can also be obtained as transformations of KumaraswamyDistribution and NoncentralBetaDistribution and is closely related to PERTDistribution, PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
), PDF[BetaDistribution[1,1],x] is equal to both PDF[UniformDistribution[],x] and PDF[PowerDistribution[1,1],x]. BetaDistribution can also be obtained as transformations of KumaraswamyDistribution and NoncentralBetaDistribution and is closely related to PERTDistribution, PearsonDistribution, ChiSquareDistribution, GammaDistribution, FRatioDistribution, and BetaPrimeDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a beta distribution:
Compare the histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare a density histogram of the sample with the PDF of the estimated distribution:
Skewness varies with shape parameters:
When both parameters go to ![]() , the distribution becomes symmetric:
, the distribution becomes symmetric:
Kurtosis varies with shape parameters:
In the limit, the kurtosis becomes the same as for NormalDistribution:
Different moments with closed forms as functions of parameters:
Consistent use of Quantity in parameters expands them into their numeric values:
Applications (3)
Cloud duration approximately follows a beta distribution with parameters 0.3 and 0.4 for a particular location. Find the probability that cloud duration will be longer than half a day:
Simulate the fraction of the day that is cloudy over a period of one month:
Find the average cloudiness duration for a day:
Find the probability of having exactly 20 days in a month with cloud duration less than 10%:
Find the probability of at least 20 days in a month with cloud duration less than 10%:
Beta distribution can be used to model the proportion of the stocks that increase in value on a given day. Fit beta distribution to the Dow Jones Industrial stocks data:
Number of days for each financial entity:
Extract values from time series for each entity and normalize numeric quantities:
Check if each entity has the same length of data:
Calculate the daily ratio of companies with an increase in value:
Find fit, excluding days with no companies having an increase in value:
Compare the histogram of the data with the PDF of the estimated distribution:
Find the probability that at least 60% of Dow Jones Industrial stocks will increase in value:
Find the average percentage of Dow Jones Industrial stocks that will increase in value:
Simulate the percentage of Dow Jones Industrial stocks that will increase in value for 30 days:
Discrete-time Markov chain ![]() , where
, where ![]() is the sequence of independent and identically distributed (iid) standard uniform random variables, and
is the sequence of independent and identically distributed (iid) standard uniform random variables, and ![]() is the sequence of iid Bernoulli random variables with success probability of
is the sequence of iid Bernoulli random variables with success probability of ![]() converges to stationary distribution BetaDistribution[p,1-p] for any initial condition
converges to stationary distribution BetaDistribution[p,1-p] for any initial condition ![]() such that
such that ![]() :
:
Sample a realization of the Markov chain and discard the burn-in portion of the path:
Samples from the Markov chain are not independent and exhibit internal structure:
Compare the histogram of path values to the PDF of the Markov chain's stationary distribution:
Properties & Relations (21)
If a variate ![]() follows beta distribution, then
follows beta distribution, then ![]() follows the reflected distribution:
follows the reflected distribution:
Relationships to other distributions:
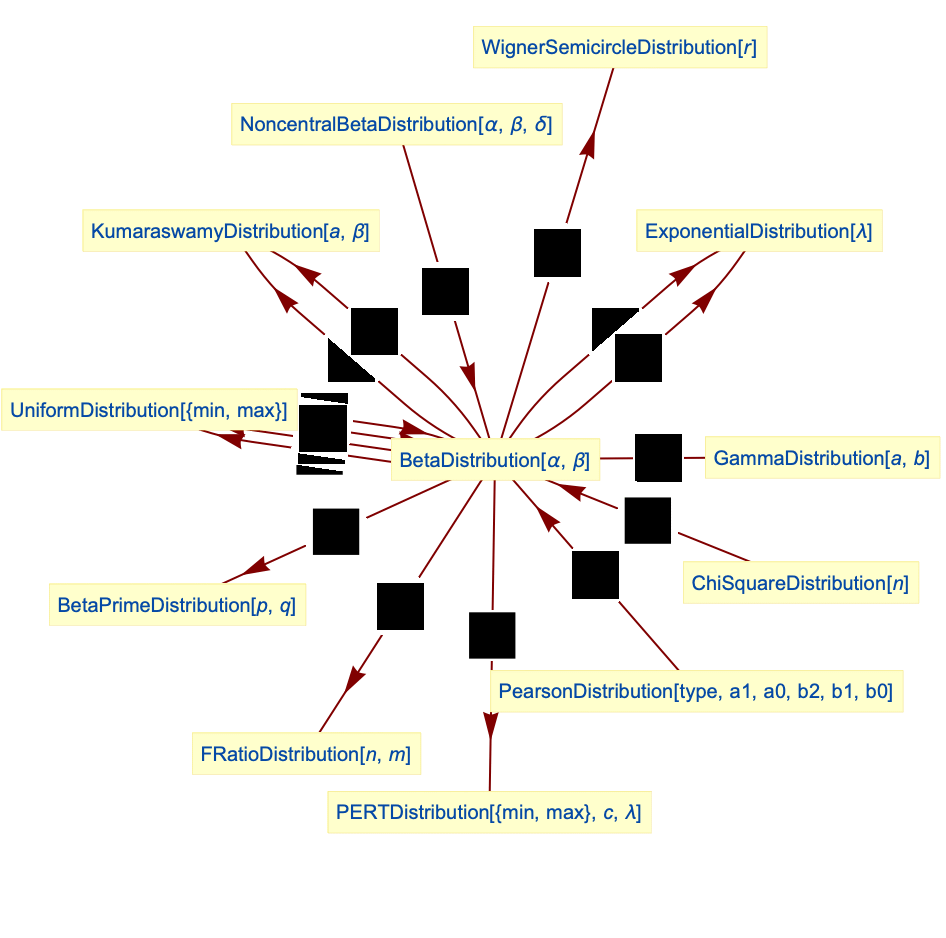
BetaDistribution[1,1] is equivalent to UniformDistribution[{0,1}]:
BetaDistribution is a transformation of UniformDistribution:
UniformDistribution is a transformation of BetaDistribution:
BetaDistribution is a limiting case of NoncentralBetaDistribution:
BetaPrimeDistribution can be obtained as a transformation of the beta-distributed variable:
Beta distribution is a special case of PearsonDistribution of type 1:
Beta distribution can be obtained as a transformation of GammaDistribution:
Beta distribution can be obtained as a transformation of ChiSquareDistribution:
FRatioDistribution can be obtained from beta distribution:
Beta distribution is an order distribution of variables from UniformDistribution:
ExponentialDistribution is a limit of a scaled beta distribution:
ExponentialDistribution is a transformation of beta distribution:
KumaraswamyDistribution is a transformation of beta distribution:
KumaraswamyDistribution simplifies to a special case of beta distribution:
PERTDistribution is a transformation of beta distribution:
WignerSemicircleDistribution is a transformation of special beta distribution:
Univariate marginals of DirichletDistribution have beta distribution:
BetaBinomialDistribution is a mixture of BinomialDistribution and BetaDistribution:
BetaNegativeBinomialDistribution is a mixture of NegativeBinomialDistribution and BetaDistribution:
Possible Issues (2)
BetaDistribution is not defined when either α or β is not a positive real number:
Substitution of invalid parameters into symbolic outputs gives results that are not meaningful:
See Also
GammaDistribution BinomialDistribution Beta BetaRegularized InverseBetaRegularized FRatioDistribution DirichletDistribution
Function Repository: MeanSpreadBetaDistribution
Tech Notes
Related Guides
Text
Wolfram Research (2007), BetaDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BetaDistribution.html (updated 2016).
CMS
Wolfram Language. 2007. "BetaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BetaDistribution.html.
APA
Wolfram Language. (2007). BetaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaDistribution.html
BibTeX
@misc{reference.wolfram_2025_betadistribution, author="Wolfram Research", title="{BetaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BetaDistribution.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_betadistribution, organization={Wolfram Research}, title={BetaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BetaDistribution.html}, note=[Accessed: 09-March-2026]}