represents the Yule distribution with shape parameter α.
represents the Waring distribution with shape parameters α and β.


WaringYuleDistribution
represents the Yule distribution with shape parameter α.
represents the Waring distribution with shape parameters α and β.
Details
- WaringYuleDistribution[α] is also known as the Yule–Simon distribution.
- The probability for integer value
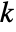 in a Waring–Yule distribution is proportional to:
in a Waring–Yule distribution is proportional to: -
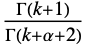
![(TemplateBox[{{k, +, 1}}, Gamma])/(TemplateBox[{{k, +, alpha, +, 2}}, Gamma]) (TemplateBox[{{k, +, 1}}, Gamma])/(TemplateBox[{{k, +, alpha, +, 2}}, Gamma])](Files/WaringYuleDistribution.en/3.png)
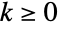
![(TemplateBox[{{k, +, beta}}, Gamma])/(TemplateBox[{{k, +, alpha, +, beta, +, 1}}, Gamma]) (TemplateBox[{{k, +, beta}}, Gamma])/(TemplateBox[{{k, +, alpha, +, beta, +, 1}}, Gamma])](Files/WaringYuleDistribution.en/5.png)
- WaringYuleDistribution allows α and β to be any positive real numbers.
- WaringYuleDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- WaringYuleDistribution[α,β] represents a discrete statistical distribution defined for integer values
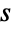 and determined by the positive real parameters α and β (called "shape parameters"). The Waring–Yule distribution has a probability density function (PDF) that is discrete and monotone decreasing, and whose overall shape (its spread and its steepness) is determined by the values of α and β. The Waring–Yule distribution is sometimes referred to as the Waring distribution, while the one-parameter form WaringYuleDistribution[α] equivalent to WaringYuleDistribution[α,1] is typically referred to as either the Yule distribution or Yule–Simon distribution.
and determined by the positive real parameters α and β (called "shape parameters"). The Waring–Yule distribution has a probability density function (PDF) that is discrete and monotone decreasing, and whose overall shape (its spread and its steepness) is determined by the values of α and β. The Waring–Yule distribution is sometimes referred to as the Waring distribution, while the one-parameter form WaringYuleDistribution[α] equivalent to WaringYuleDistribution[α,1] is typically referred to as either the Yule distribution or Yule–Simon distribution. - Despite Waring's work dating to the eighteenth century, the history of the Waring–Yule distribution essentially dates to the genesis of the one-parameter Yule–Simon distribution, which was first given comprehensive treatment by H. A. Simon in the mid-1950s and was named (by Simon) for British statistician G. U. Yule, due to Yule's 1925 discovery and application of the distribution to stochastic processes related to behavioral evolution. The two-parameter generalization mentioned above dates to the work of Irwin in the early 1960s, and in the decades since, many generalizations of the Waring–Yule distribution have been discovered and explored. Such generalizations have been used to describe phenomena related to network analysis, pharmaceutical science, and accident theory.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Waring–Yule distribution. Distributed[x,WaringYuleDistribution[α,β]], written more concisely as xWaringYuleDistribution[α,β], can be used to assert that a random variable x is distributed according to a Waring–Yule distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[WaringYuleDistribution[α,β],x] and CDF[WaringYuleDistribution[α,β],x], though one should note that there is no closed-form expression for its PDF. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. These quantities can be visualized using DiscretePlot.
- DistributionFitTest can be used to test if a given dataset is consistent with a Waring–Yule distribution, EstimatedDistribution to estimate a Waring–Yule parametric distribution from given data, and FindDistributionParameters to fit data to a Waring–Yule distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Waring–Yule distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Waring–Yule distribution.
- TransformedDistribution can be used to represent a transformed Waring–Yule distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Waring–Yule distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Waring–Yule distributions.
- WaringYuleDistribution is related to a number of other statistical distributions. It is a special case of BetaNegativeBinomialDistribution, in the sense that the PDF of WaringYuleDistribution[α,β] is precisely the same as that of BetaNegativeBinomialDistribution[α,β,1]. Moreover, WaringYuleDistribution can be realized as a parameter mixture (ParameterMixtureDistribution) of GeometricDistribution and UniformDistribution, in the sense that the PDF of WaringYuleDistribution[a] is equivalent to that of GeometricDistribution[w1/a] for wUniformDistribution[] (when
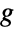 ). WaringYuleDistribution is also closely related to PoissonDistribution, PoissonConsulDistribution, and PolyaAeppliDistribution.
). WaringYuleDistribution is also closely related to PoissonDistribution, PoissonConsulDistribution, and PolyaAeppliDistribution.
Examples
open all close allBasic Examples (4)
Scope (9)
Cumulative distribution function of Yule distribution:
Cumulative distribution function of Waring distribution:
Generate a sample of pseudorandom numbers from a Waring distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness for Yule distribution:
Find where the skewness attains its minimum:
Skewness for Waring distribution:
Kurtosis for Yule distribution:
Find where the kurtosis attains its minimum:
Kurtosis for Waring distribution:
Different moments with closed forms as functions of parameters:
Moment for Yule distribution:
CentralMoment for Yule distribution:
FactorialMoment for Yule distribution:
Cumulant for Yule distribution:
Moment for Waring distribution:
CentralMoment for Waring distribution:
FactorialMoment for Waring distribution:
Cumulant for Waring distribution:
Applications (3)
The CDF of WaringYuleDistribution is an example of a right-continuous function:
Creation of new species within genera occurs at rate ![]() , while birth of new genera occurs at a slower rate
, while birth of new genera occurs at a slower rate ![]() . Limiting frequency distribution of sizes of genera of all ages is given by WaringYuleDistribution. Assuming
. Limiting frequency distribution of sizes of genera of all ages is given by WaringYuleDistribution. Assuming ![]() :
:
Plot the logarithm of the PDF:
Find the probability that a genus will have no more than 5000 species:
Generate a collection of words by randomly selecting characters and white space. The resulting word sizes can be modeled using a WaringYuleDistribution:
Properties & Relations (5)
Relationships to other distributions:
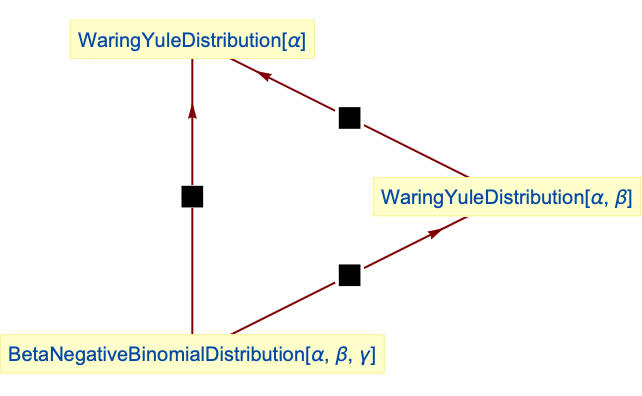
Yule distribution is a special case of BetaNegativeBinomialDistribution:
Waring distribution is a special case of BetaNegativeBinomialDistribution:
Waring distribution simplifies to Yule distribution for β=1:
Yule distribution can be obtained as a parameter mixture of GeometricDistribution and UniformDistribution:
Related Guides
History
Text
Wolfram Research (2010), WaringYuleDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/WaringYuleDistribution.html.
CMS
Wolfram Language. 2010. "WaringYuleDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaringYuleDistribution.html.
APA
Wolfram Language. (2010). WaringYuleDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaringYuleDistribution.html
BibTeX
@misc{reference.wolfram_2025_waringyuledistribution, author="Wolfram Research", title="{WaringYuleDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaringYuleDistribution.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_waringyuledistribution, organization={Wolfram Research}, title={WaringYuleDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/WaringYuleDistribution.html}, note=[Accessed: 24-February-2026]}