represents a Lindley distribution with shape parameter δ.


LindleyDistribution
represents a Lindley distribution with shape parameter δ.
Details
- The probability density for value
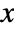 is proportional to
is proportional to 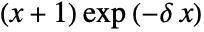 for
for 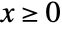 , and is zero for
, and is zero for 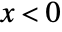 .
. - LindleyDistribution allows δ to be any positive real number.
- LindleyDistribution allows δ to be a dimensionless quantity. »
- LindleyDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- LindleyDistribution[δ] represents a statistical distribution supported on the interval
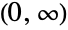 and parametrized by a positive real number δ (called a "shape parameter") that determines the overall behavior of its probability density function (PDF). Depending on the parameter δ, the PDF of a Lindley distribution may be either unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with a potential singularity approaching the lower boundary of its domain. In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than algebraically for large values of
and parametrized by a positive real number δ (called a "shape parameter") that determines the overall behavior of its probability density function (PDF). Depending on the parameter δ, the PDF of a Lindley distribution may be either unimodal with a single "peak" (i.e. a global maximum) or monotone decreasing with a potential singularity approaching the lower boundary of its domain. In addition, the tails of the PDF are "thin" in the sense that the PDF decreases exponentially rather than algebraically for large values of 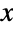 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) Experts note that the Lindley distribution is qualitatively similar to the exponential distribution (ExponentialDistribution), and while the term "Lindley–Exponential distribution" is sometimes used to refer to a generalization of the Lindley distribution, one should note that the Lindley and exponential distributions are, in fact, distinct.
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) Experts note that the Lindley distribution is qualitatively similar to the exponential distribution (ExponentialDistribution), and while the term "Lindley–Exponential distribution" is sometimes used to refer to a generalization of the Lindley distribution, one should note that the Lindley and exponential distributions are, in fact, distinct. - The Lindley distribution was developed by British statistician D. V. Lindley in a paper published in 1958 and was expressed therein merely as an example of a larger theoretical investigation of so-called fiducial distributions (distributions that are "inverse" to known distributions in a very precise way) relative to Bayesian analysis. The properties of distribution itself remained relatively unstudied until a 2008 publication by Ghitany et al., but even so, the Lindley distribution has been used to model real-world data such as customer waiting times and has been generalized so as to model a wide spectrum of phenomena including cancer patient survival, stress factors and reliability statistics, carbon retained by plant leaves, and miscellaneous lifetime data.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Lindley distribution. Distributed[x,LindleyDistribution[δ]], written more concisely as xLindleyDistribution[δ], can be used to assert that a random variable x is distributed according to a Lindley distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Lindley distributions may be given using PDF[LindleyDistribution[δ],x] and CDF[LindleyDistribution[δ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Lindley distribution, EstimatedDistribution to estimate a Lindley parametric distribution from given data, and FindDistributionParameters to fit data to a Lindley distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Lindley distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Lindley distribution.
- TransformedDistribution can be used to represent a transformed Lindley distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Lindley distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Lindley distributions.
- LindleyDistribution is related to a number of other distributions including the above-mentioned qualitative similarities with ExponentialDistribution. Moreover, Ghitany et al. demonstrated that LindleyDistribution can be written as a special mixture of ExponentialDistribution and GammaDistribution in the sense that the PDF
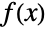 of LindleyDistribution[δ] can be written as a linear combination of the PDFs of ExponentialDistribution[δ] and GammaDistribution[2,δ]. In addition, LindleyDistribution has been generalized so as to share quantitative properties with a number of well-known distributions including PoissonDistribution, BetaDistribution, ExponentialDistribution, and PowerDistribution.
of LindleyDistribution[δ] can be written as a linear combination of the PDFs of ExponentialDistribution[δ] and GammaDistribution[2,δ]. In addition, LindleyDistribution has been generalized so as to share quantitative properties with a number of well-known distributions including PoissonDistribution, BetaDistribution, ExponentialDistribution, and PowerDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Lindley distribution:
Compare its histogram to the PDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends on the shape parameter δ:
Kurtosis depends on the shape parameter δ:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Closed form for symbolic order:
Use dimensionless Quantity to define LindleyDistribution:
Applications (2)
LindleyDistribution is used to create a discrete Poisson–Lindley distribution:
Cumulative distribution function:
Mean is the same as for LindleyDistribution:
Poisson–Lindley distribution can be used to model insurance claim counts:
Estimate parameters based on claim amounts:
The fit is better than using just PoissonDistribution:
Related Guides
Text
Wolfram Research (2010), LindleyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/LindleyDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "LindleyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LindleyDistribution.html.
APA
Wolfram Language. (2010). LindleyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LindleyDistribution.html
BibTeX
@misc{reference.wolfram_2025_lindleydistribution, author="Wolfram Research", title="{LindleyDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/LindleyDistribution.html}", note=[Accessed: 05-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_lindleydistribution, organization={Wolfram Research}, title={LindleyDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/LindleyDistribution.html}, note=[Accessed: 05-March-2026]}