ParameterMixtureDistribution

ParameterMixtureDistribution[dist[θ],θwdist]

代表一个参数混合分布. 其中参数 θ 按照权重分布 wdist 而分布.

ParameterMixtureDistribution[dist[θ1,θ2,…],{θ1wdist1,θ2wdist2,…}]

代表一个参数混合分布. 其中参数 θ1 的权重分布为 wdist1，参数 θ2 的权重分布为 wdist2 等等.

更多信息和选项

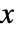  • 值的概率分布密度由 Expectation[PDF[dist[θ],x],θwdist] 给出.
  • 权重分布 wdist 的区域必须与 dist[θ] 所期望的参数域相等或是它的一个子集.
  • 参数 θi 可以是离散的也可以是连续的.
  • 可以用选项 Assumptionsassum 来指定对参数的假设.
  • ParameterMixtureDistribution 可用于诸如 Mean、CDF 和 RandomVariate 等等的函数.

范例

打开所有单元关闭所有单元

基本范例  (3)

指定一个参数混合分布：

参数混合分布与其它任何分布有相同的功能：

寻找一个多变量分布的参数混合：

范围  (36)

基本用途  (7)

求 ExponentialDistribution 均匀权重分布下的参数混合：

概率密度函数：

权重域必须满足主分布的参数假设：

采用一个正实数上的权重分布：

得到的参数混合累积分布函数（CDF）为：

将一个离散的权重用于一个离散的参数：

比较概密度函数：

比较从各分布得到小于 4 的值的概率：

只改变一个参数：

只改变一个参数：

均值与方差：

用一个多变量分布作为权重来改变多个参数：

用多个权重分布来改变多个参数：

图示概率密度函数：

估计一个参数混合分布中的参数：

创建一个随机取样作为权重分布参数的一个选择：

找出分布参数：

比较取样的直方图与估计分布的概率分布函数：

权重分布  (5)

定义一个具有连续单变量权重分布的参数混合：

定义一个具有离散单变量权重分布的参数混合：

求概率密度函数：

对于符号式阶数， Moment 有闭形式：

定义一个具有离散单变量权重分布的参数混合：

概率密度函数：

定义一个具有多变量权重分布的参数混合：

概率密度函数：

验证概率分布函数的积分为 1：

应用多个权重分布：

均值：

方差:

参数分布  (8)

定义一个连续单变量分布的参数混合：

累积分布函数：

找出一个连续单变量分布的一个混合：

概率密度函数：

定义一个离散单变量分布的参数混合：

生成一个随机取样：

求平均值和方差：

求一个离散单变量分布的一个参数混合：

概率密度函数：

平均值与方差：

对于 的一个确定的值，Moment 对于符号式阶数有闭形式：

定义一个二变量连续分布的一个参数混合：

用一个随机取样和一个光滑直方图来图示密度函数：

定义一个二变量分布的一个参数混合：

概率密度函数：

均值：

协方差矩阵：

求一个多变量离散分布的一个参数混合分布:

生成一个随机样本：

各分量直方图：

LaplaceDistribution 可以用参数混合来表示：

非参数分布  (3)

使用 EmpiricalDistribution 作为一个权：

概率密度函数：

使用 HistogramDistribution 作为一个权：

概率密度函数：

定义一个以 SmoothKernelDistribution 为权的参数混合：

绘制概率密度函数：

绘制累积分布函数：

导出分布  (11)

使用一个 ProductDistribution 作为一个参数混合的一个权重分布：

利用从 随机抽样的点绘制的直方图来可视化概率密度函数（PDF）：

找出一个 TransformedDistribution 的参数混合分布：

用随机抽样将密度函数可视化：

用一个 TransformedDistribution 作为权重分布，寻找一个参数混合：

概率密度函数：

利用一个 MixtureDistribution 作为一个参数混合中的一个权重分布：

概率密度函数：

均值和方差：

让一个 MixtureDistribution 中的权重按照一个概率分布变化；

概率密度函数：

与取平均值的不变权重的 MixtureDistribution 比较：

两个密度函数是相等的：

定义 TruncatedDistribution 的一个参数混合：

均值和方差：

定义 TruncatedDistribution 的一个参数分布：

用随机抽样将概率密度函数可视化

用一个 TruncatedDistribution 作为一个参数混合中的一个权重分布：

概率分布函数：

均值：

找出一个 OrderDistribution 的参数混合分布：

概率密度函数：

用一个 OrderDistribution 作为一个权重分布：

概率密度函数：

QuantityDistribution 的参数混合分布还是 QuantityDistribution：

自动简化  (2)

离散分布  (1)

以 BetaDistribution 为权的参数混合：

包含 PoissonDistribution 的参数混合：

连续分布  (1)

包含 RayleighDistribution 的参数分布：

包含 RayleighDistribution 的参数分布：

选项  (1)

Assumptions  (1)

WaringYuleDistribution 是几何分布和 UniformDistribution 的参数混合分布：

和内置答案比较：

应用  (7)

SuzukiDistribution 被定义为 RayleighDistribution 与 LogNormalDistribution 的参数混合：

KDistribution 可以表示为 RayleighDistribution 和 GammaDistribution 的一个参数混合：

银行柜员服务顾客所花费的分钟数遵循 ExponentialDistribution， 其中平均时间 具有平均值为 3 的 LindleyDistribution. 求服务时间分布：

概率分布函数：

平均服务时间：

模拟后面30个顾客的服务时间：

在一个光通讯系统中，传输的光在接收器中产生电流. 电子的数目遵循一个泊松分布和另外一个分布的参数混合，取决于光的类型. 如果光源使用强度为 的相干的激光，则电子数目分布是一个泊松分布：

这是一个 PoissonDistribution:

如果光源使用热照明，则泊松参数遵循参数为 的 ExponentialDistribution， 电子数分布可确定如下：

这两个分布明显不同，可用以确定光源的类型:

福格特谱线性式是一个多普勒谱形和一个洛伦兹谱形相结合的结果：

计算密度函数：

画出密度函数图：

计算谱半宽：

定义修正的正态分布：

绘制 取某几个值时修正的正态分布密度的图形，并与标准的正态分布密度比较：

定义多变量 Pólya 分布：

概率密度函数：

属性和关系  (4)

一个参数混合的概率密度函数可以用 Expectation 来计算：

具有离散权的参数混合，假设值的有限数可以表示为一个 MixtureDistribution：

比较概率密度函数：

具有离散权的参数混合，假设值的可计数数可以被 MixtureDistribution 近似：

比较以不同分位数作为截止的近似：

通过 MixtureDistribution 近似一个具有连续权的参数混合：

比较概率密度函数：

Wolfram Research (2010)，ParameterMixtureDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html （更新于 2016 年）.

文本

Wolfram Research (2010)，ParameterMixtureDistribution，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "ParameterMixtureDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html.

APA

Wolfram 语言. (2010). ParameterMixtureDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html 年

BibTeX

@misc{reference.wolfram_2024_parametermixturedistribution, author="Wolfram Research", title="{ParameterMixtureDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_parametermixturedistribution, organization={Wolfram Research}, title={ParameterMixtureDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/ParameterMixtureDistribution.html}, note=[Accessed: 22-November-2024 ]}