WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

PearsonCorrelationTest

PearsonCorrelationTest[v₁,v₂]

ベクトル v₁ と v₂ が線形独立かどうかの検定を行う．

PearsonCorrelationTest[…,"property"]

"property"の値を返す．

詳細とオプション

PearsonCorrelationTestは，v₁と v₂に対して，ベクトルが線形独立であるという帰無仮説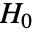と，そうではないという対立仮説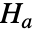で仮説検定を行う．
デフォルトで，確率の値すなわち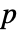値が返される．
小さい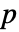値は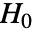が真である確率が低いことを示唆する．
引数 v₁と v₂は任意の実数値で同じ長さのベクトルでよい．
PearsonCorrelationTestはCorrelation[v₁,v₂]で計算されたピアソン(Pearson)積率相関係数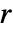に基づいている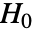．の下では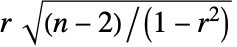，はStudentTDistribution[n-2]に漸近的に従う．
PearsonCorrelationTest[v₁,v₂,"HypothesisTestData"]は，htd["property"]として追加的な検定結果と特性の抽出に使うことができるHypothesisTestDataオブジェクト htd を返す．
PearsonCorrelationTest[v₁,v₂,"property"]を直接使って"property"の値を与えることができる．
検定結果のレポートに関連する特性

	"DegreesOfFreedom"	検定に使われる自由度
	"PValue"	検定の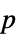値
	"PValueTable"	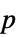値を含むフォーマットされた表
	"ShortTestConclusion"	検定結果の短い記述
	"TestConclusion"	検定結果の記述
	"TestData"	検定統計量と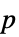値を含むリスト
	"TestDataTable"	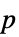値と検定統計量のフォーマットされた表
	"TestStatistic"	検定統計量
	"TestStatisticTable"	検定統計量を含むフォーマットされた表

使用可能なオプション

	AlternativeHypothesis	"Unequal"	対立仮説のための不等式
	Method	Automatic	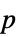値の計算に使うメソッド
	SignificanceLevel	0.05	診断とレポートのための切捨て
	VerifyTestAssumptions	Automatic	証明する仮定

独立性の検定については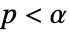，のときにのみ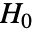が拒絶されるような切捨て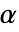が選ばれる．"TestConclusion"特性と"ShortTestConclusion"特性に使われる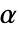の値はSignificanceLevelオプションで制御される．値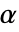は正規性の診断検定にも使われる．デフォルトで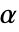，は0.05に設定されている．
IndependenceTestにおけるVerifyTestAssumptionsの名前付き設定
"Normality" すべてのデータが正規分布に従っていることを証明する

例題

すべて開くすべて閉じる

例 (1)

2つのベクトルが独立かどうかの検定を行う：

スコープ (7)

検定 (4)

2つのベクトルが独立かどうかの検定を行う：

ベクトルが独立のとき，値は一般に大きくなる：

ベクトルが従属関係にあるときは，値は一般に小さくなる：

繰り返して特性を抽出するためのHypothesisTestDataオブジェクトを作る：

抽出可能な特性：

HypothesisTestDataオブジェクトから特性をいくつか抽出する：

検定からの値と検定統計量：

任意数の特性を同時に抽出する：

値と検定統計量，そして自由度：

レポート (3)

検定からの結果を表にする：

検定結果の表：

カスタマイズしたレポートのために検定の表から項目を読み出す：

値あるいは検定統計量を表にする：

表からの値：

表からの検定統計量：

オプション (12)

AlternativeHypothesis (2)

デフォルトで両側検定が行われる：

両側検定を行う．あるいは片側検定を代りに行う：

両側検定：

代りの2つの片側検定：

Method (4)

デフォルトで，値は漸近的な検定統計分布を使って計算される：

置換法を使って値を求めることができる：

使用する置換回数を設定する：

デフォルトで，回のランダムな置換が行われる：

ランダムな置換の生成に使うシードを設定する：

SignificanceLevel (3)

診断検定の有意水準を設定する：

デフォルトで0.05が使われる．2つの検定が行われたので，このメッセージは0.025となっている：

有意水準を設定すると自動的に選ばれる検定が変わることがある：

デフォルトではノンパラメトリック検定が選ばれたはずである：

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

VerifyTestAssumptions (3)

デフォルトで適切な場合には正規性の検定が行われる：

AllあるいはNoneを使って診断をまとめて制御することができる：

すべての仮定を検証する：

仮定はチェックしない：

診断は個々に制御することができる：

正規性についてチェックする：

診断結果を明示的に設定する：

特性と関係 (7)

検定統計はCorrelationに等しい：

の下では，検定統計はStudentTDistribution[n-2]に漸近的に従う：

正規分布ではない分布にはSpearmanRankTestを使う：

Spearmanのに基づいた検定の方が検定サイズの保存に関してはよい結果を出す：

推定と観測による検定サイズの表：

IndependenceTestを使って適切な検定を自動的に選ぶことができる：

CorrelationTestを使っての特定の値についての検定を行う：

ピアソンの相関検定は，入力がTimeSeriesのときにのみ’値に使うことができる：

ピアソンの相関検定は，入力がTemporalDataのときはすべての値に同時に使うことができる：

時間データの選択された成分を明示的に検定する：

値を直接使う：

おもしろい例題 (1)

帰無仮説が真であるときに統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

トップへ