PillaiTraceTest

PillaiTraceTest[m1,m2]

tests whether the matrices m1 and m2 are independent.

PillaiTraceTest[…,"property"]

returns the value of "property".

Details and Options

  • PillaiTraceTest performs a hypothesis test on m1 and m2 with null hypothesis 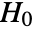that the matrices are linearly independent, and alternative hypothesis 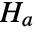that they are not.
  • By default, a probability value or 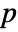-value is returned.
  • A small 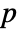-value suggests that it is unlikely that 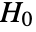is true.
  • The arguments m1 and m2 can be any real-valued vectors or matrices of equal length.
  • PillaiTraceTest is based on Pillai's trace statistic computed by PillaiTrace[m1,m2].
  • PillaiTraceTest[m1,m2,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • PillaiTraceTest[m1,m2,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in the test
    "PValue"the 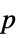-value of the test
    "PValueTable"formatted table containing the 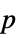-value
    "ShortTestConclusion"a short description of the conclusion of the test
    "TestConclusion"a description of the conclusion of the test
    "TestData"a list containing the test statistic and 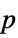-value
    "TestDataTable"formatted table of the 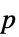-value and test statistic
    "TestStatistic"the test statistic
    "TestStatisticTable"formatted table containing the test statistic
  • The following options can be used:
  • Method Automaticthe method to use for computing 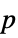-values
    SignificanceLevel 0.05cutoff for diagnostics and reporting
    VerifyTestAssumptions Automaticwhat assumptions to verify
  • For tests of independence, a cutoff 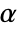is chosen such that 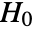is rejected only if 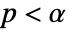. The value of 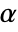used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 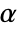is also used in diagnostic tests of normality. By default, 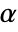is set to 0.05.
  • Named settings for VerifyTestAssumptions in IndependenceTest include:
  • "Normality"verify that all data is normally distributed

Examples

open allclose all

Basic Examples  (2)

Test whether two vectors are independent:

Test whether two matrices are independent:

At the 0.05 level, there is insufficient evidence to reject independence:

Scope  (8)

Testing  (5)

Test whether two vectors are independent:

The -values are typically large when the vectors are independent:

The -values are typically small when there are dependencies:

Test whether two matrices are independent:

The -values are typically small for dependent matrices:

The -values are typically large when matrices are independent:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from the HypothesisTestData object:

The -value and test statistic:

Extract any number of properties simultaneously:

The -value and test statistic:

Reporting  (3)

Tabulate the results from the test:

A table of the test results:

Retrieve the entries from a test table for customized reporting:

Tabulate the -value or test statistic:

The -value from the table:

The test statistic from the table:

Options  (10)

Method  (4)

By default, -values are computed using asymptotic test statistic distributions:

The -value can be obtained using permutation methods:

Set the number of permutations to use:

By default, random permutations are used:

Set the seed used for generating random permutations:

SignificanceLevel  (2)

Set the significance level for diagnostic tests:

By default, 0.05 is used. The message shows 0.025 because two tests were performed:

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

VerifyTestAssumptions  (4)

By default, normality is tested when appropriate:

Diagnostics can be controlled as a group using All or None:

Verify all assumptions:

Check no assumptions:

Diagnostics can be controlled independently:

Check for normality:

Explicitly set the diagnostic result:

It is often useful to bypass diagnostic tests for simulation purposes:

The assumptions of the test hold by design, so a great deal of time can be saved:

The results are identical:

Properties & Relations  (4)

PillaiTraceTest uses the PillaiTrace measure as a test statistic:

The -value is computed using a ChiSquareDistribution[r*s]:

PillaiTraceTest is one of the tests available to IndependenceTest:

IndependenceTest automates the choice of test:

The Pillai trace test works with the values only when the input is a TimeSeries:

The Pillai trace test works with all the values together when the input is a TemporalData:

Test selected components of the temporal data explicitly:

Use the values directly:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2012), PillaiTraceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/PillaiTraceTest.html.

Text

Wolfram Research (2012), PillaiTraceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/PillaiTraceTest.html.

CMS

Wolfram Language. 2012. "PillaiTraceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PillaiTraceTest.html.

APA

Wolfram Language. (2012). PillaiTraceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PillaiTraceTest.html

BibTeX

@misc{reference.wolfram_2025_pillaitracetest, author="Wolfram Research", title="{PillaiTraceTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/PillaiTraceTest.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_pillaitracetest, organization={Wolfram Research}, title={PillaiTraceTest}, year={2012}, url={https://reference.wolfram.com/language/ref/PillaiTraceTest.html}, note=[Accessed: 18-April-2025 ]}