Group Theory Algorithms
Group Theory Algorithms
This tutorial introduces some basic algorithms for computing with finite permutation groups, other than those introduced in "Permutation Groups".
A subgroup 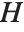 of a group
of a group  partitions the list of elements of
partitions the list of elements of  into disjoint subsets, called cosets of
into disjoint subsets, called cosets of 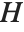 in
in  , such that
, such that 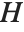 is one of them and the rest are of the form
is one of them and the rest are of the form  for some element
for some element 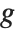 of
of  , with ⊙ denoting the product law. A way of identifying the coset is by selecting a representative from each coset, for example the smallest element in the coset.
, with ⊙ denoting the product law. A way of identifying the coset is by selecting a representative from each coset, for example the smallest element in the coset.
| RightCosetRepresentative | compute smallest group element in a coset |
The canonical representative of the right coset is taken to be the least permutation in the order defined by images:
For bigger groups, it is not possible to list or rank all permutations, but you can still use RightCosetRepresentative.
For any permutation belonging to the group itself, the canonical representative is always the identity permutation:
Check that the representative indeed belongs to the same coset. This will be the case if there exists a permutation h in the original group such that permPermutationProduct[h,rep]:
| GroupCentralizer | compute the centralizer subgroup of some group element |
The (pointwise) stabilizer of a group  is the subgroup of elements of
is the subgroup of elements of  fixing a set of one or several points of the domain of action. This concept can be extended to the setwise stabilizer, which is the subgroup of elements either fixing those points or moving them among themselves.
fixing a set of one or several points of the domain of action. This concept can be extended to the setwise stabilizer, which is the subgroup of elements either fixing those points or moving them among themselves.
| GroupSetwiseStabilizer | compute the setwise stabilizer subgroup of a list of points |