WOLFRAM

Wolfram 语言与系统参考资料中心

PermutationGroup[{perm1,…,permn}]

表示由置换 perm1,…,permn 相乘生成的群.Null

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
应用  
属性和关系  
巧妙范例  
参见
技术笔记
相关指南
历史
按以下格式引用：

PermutationGroup

PermutationGroup[{perm1,…,permn}]

表示由置换 perm1,…,permn 相乘生成的群.Null

更多信息

  • 生成置换 permi 必须以不相交轮换的形式给出，且头部必须是 Cycles.
  • 置换群的性质通常是通过用Schreier–Sims 算法构建群的强生成集表示来计算的.

范例

打开所有单元 关闭所有单元

基本范例  (1)

有两个生成元定义的置换群：

计算其阶数：

范围  (3)

一个空的生成元列表表示恒等（或平庸，或中立）群：

找出由两个置换生成的群的阶数：

测试具有相同的支撑但可能由不同的置换生成的群的相等与否：

作为 Wolfram 语言表达式它们是不同的：

应用  (2)

这是一个表示正 边形的所有转动和反射的群，即二面体群 群在 时的情形. 它可以由一个角度为 的转动和一个沿着通过顶点的一个轴的反射生成：

依照每一个群元素构造八边形：

这是原始八边形和它的七个转动. 数字沿逆时针方向增加：

这是沿1-5 平分线反射的八边形和它的七个转动. 数字沿顺时针方向增加：

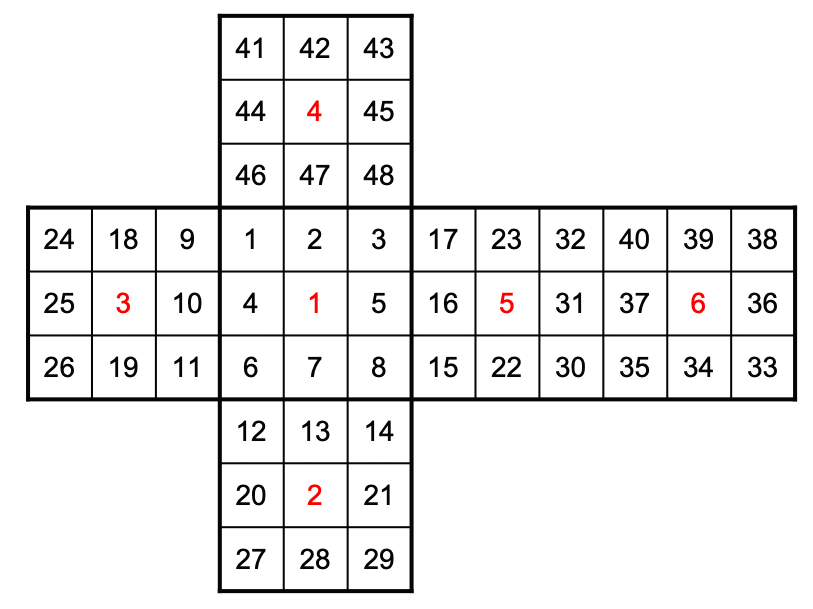
图形的自同构群用 PermutationGroup 表示：

以下为该图形的自同构数量：

属性和关系  (3)

一个被命名群的显式表示：

用 个对换生成 次对称群：

用 个生成元生成 次交错群：

巧妙范例  (1)

Rubik 魔方的移动形成一个群. 用数字1到48为魔块儿编号：

这是六个基本的转动：

群阶：

对换相邻的两个棱魔块儿是不允许的：

同时对换两个棱魔块儿对是允许的：

这是超翻（苏perflip）移动，即同时对换所有棱魔块儿对而保持所有角不变：

棱和角不可能混合（因为群对魔方的作用是不可传递的），但任何两个角或任何两个边可以对换：

Wolfram Research (2010)，PermutationGroup，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PermutationGroup.html.

文本

Wolfram Research (2010)，PermutationGroup，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PermutationGroup.html.

CMS

Wolfram 语言. 2010. "PermutationGroup." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationGroup.html.

APA

Wolfram 语言. (2010). PermutationGroup. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PermutationGroup.html 年

BibTeX

@misc{reference.wolfram_2025_permutationgroup, author="Wolfram Research", title="{PermutationGroup}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationGroup.html}", note=[Accessed: 31-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_permutationgroup, organization={Wolfram Research}, title={PermutationGroup}, year={2010}, url={https://reference.wolfram.com/language/ref/PermutationGroup.html}, note=[Accessed: 31-October-2025]}