PermutationMatrix
PermutationMatrix[permv]
置換ベクトル permv によって構造化配列として与えられる置換行列を表す.
PermutationMatrix[pmat]
置換行列 pmat を構造化配列に変換する.
詳細とオプション



- 置換行列は,構造化配列として表現されるときは,Det,Inverse,LinearSolve等でより効率的な格納と動作を可能にする.
- 置換行列は,一般に,行列分解アルゴリズムの出力に,(コンテキスト内で通常ピボットと呼ばれる)行または列の置換を表すために出現する.
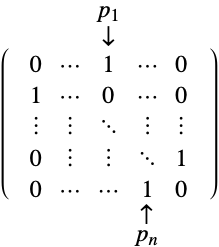
- 置換ベクトル
 が与えられた場合,結果の置換行列
が与えられた場合,結果の置換行列 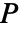 は
は ![P〚i,j〛=TemplateBox[{{i, ,, {p, _, j}}}, KroneckerDeltaSeq] P〚i,j〛=TemplateBox[{{i, ,, {p, _, j}}}, KroneckerDeltaSeq]](Files/PermutationMatrix.ja/4.png) で与えられる.これは,行
で与えられる.これは,行 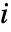 の列
の列 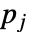 が1でそれ以外はすべて0の行列に相当する.
が1でそれ以外はすべて0の行列に相当する. - 置換行列
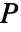 を使って左の
を使って左の 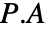 から乗算することで行を,あるいは右の
から乗算することで行を,あるいは右の ![A.TemplateBox[{P}, Transpose] A.TemplateBox[{P}, Transpose]](Files/PermutationMatrix.ja/10.png) からの転置を乗算することで列を置換することができる.
からの転置を乗算することで列を置換することができる. - 置換行列
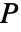 は,逆行列が転置
は,逆行列が転置 ![P^(-1)=TemplateBox[{P}, Transpose] P^(-1)=TemplateBox[{P}, Transpose]](Files/PermutationMatrix.ja/12.png) に等しい直交行列である.
に等しい直交行列である. - 置換行列は行列の乗算のもとで閉じているので,
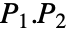 もまた置換行列である.
もまた置換行列である. - 置換行列の行列式は
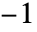 か1のどちらかで,Signature[permv]に等しい.
か1のどちらかで,Signature[permv]に等しい. - 以下の操作はPermutationMatrixについて高速化される.
-
Det 時間 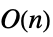
Dot 時間 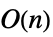
Inverse 時間 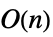
LinearSolve 時間 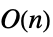
- PermutationMatrix sa については,以下の特性"prop"に sa["prop"]でアクセスできる.
-
"PermutationCycles" 置換行列の互いに素な巡回表現 "PermutationList" 置換行列の置換リスト表現 "WorkingPrecision" 内部的に使う精度 "Properties" サポートされる特性のリスト "Structure" 構造化配列の型 "StructuredData" 構造化配列で保存されている内部データ "StructuredAlgorithms" 構造化配列についての特別なメソッドを持つ関数のリスト "Summary" Datasetとして表されるまとめ情報 - Normal[PermutationMatrix[a,…]]は通常の行列としての置換行列を与える.
- 次は,使用可能なオプションである.
-
TargetStructure Automatic 返される行列の構造 WorkingPrecision Infinity 成分を作成する精度 - 次は,TargetStructureの可能な設定である.
-
Automatic 返す表現を自動選択する "Dense" 行列を密な行列として表す "Orthogonal" 行列を直交行列として表す "Sparse" 行列を疎な配列として表す "Structured" 行列を構造化配列として表す "Unitary" 行列をユニタリ行列として表す - PermutationMatrix[…,TargetStructureAutomatic]はPermutationMatrix[…,TargetStructure"Structured"]に等しい.
例題
すべて開くすべて閉じるスコープ (7)
TwoWayRule(交換置換)から置換行列を構築する:
PermutationMatrixオブジェクトは配列についての情報を与える特性を含む:
"PermutationList"は,もとになっている置換の互いに素な巡回表現を与える:
"PermutationList"は置換リスト表現を与える:
"WorkingPrecision"は,行列成分の精度を与える:
"Summary"特性は配列についての情報の簡単なまとめを与える:
"StructuredAlgorithms"特性は構造化アルゴリズムを持つ関数のリストを与える:
構造化アルゴリズムは,適切な場合は別のPermutationMatrixオブジェクトを返す:
これはInversePermutationの結果と等しい:
オプション (2)
アプリケーション (4)
これはGroupMultiplicationTableの結果と等価である:
行列の列を積み上げて1つのベクトルにするvec演算子を定義する:
vec置換行列はvec演算子を行列に適用した結果とその転置を関連付ける:
vec置換行列を使って指定された2つの行列のクロネッカー(Kronecker)積と同じ行列を逆順にしたもののクロネッカー積の関係を表すことができる:
高速フーリエ変換(FFT)の効率は2つの小さいフーリエ行列から1つの大きいフーリエ行列が形成できる点にかかっている.大きさが p と q の2つの小さいフーリエ行列を生成する:
大きさが p q のフーリエ行列はより単純な4つの行列の積として表すことができる:
結果の行列がFourierMatrixの結果に等しいことを示す:
ベクトルの離散フーリエ変換はフーリエ行列の因子を連続的にベクトルに掛けることで計算できる:
結果はベクトルにFourierを適用したものに等しい:
特性と関係 (6)
PermutationMatrix[p<->q]はPermutationMatrix[Cycles[{{p,q}}]]に等しい:
SparseArray[PermutationMatrix[…]]を使ってSparseArrayとしての表現を得る:
置換リストを左から掛けることは置換リストにPartを使うことと等価である:
置換行列を左から掛けることは置換行列にPermuteを使うことと等価である:
テキスト
Wolfram Research (2022), PermutationMatrix, Wolfram言語関数, https://reference.wolfram.com/language/ref/PermutationMatrix.html (2024年に更新).
CMS
Wolfram Language. 2022. "PermutationMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PermutationMatrix.html.
APA
Wolfram Language. (2022). PermutationMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationMatrix.html