QBinomial

QBinomial[n,m,q]

gives the -binomial coefficient .

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • .
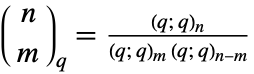  • QBinomial automatically threads over lists.

Examples

open allclose all

Basic Examples  (6)

Exact evaluation with numbers:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Use FunctionExpand to obtain Gaussian polynomials:

Scope  (20)

Numerical Evaluation  (5)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute the elementwise values of an array:

Or compute the matrix QBinomial function using MatrixFunction:

Specific Values  (5)

QBinomial for symbolic parameters:

Value at zero:

Find the minimum of QBinomial[3,2,q]:

QBinomial threads elementwise over lists:

TraditionalForm formatting:

Visualization  (2)

Plot the QBinomial function for various parameters:

Plot the real part of TemplateBox[{3, 2, z}, QBinomial]:

Plot the imaginary part of TemplateBox[{3, 2, z}, QBinomial]:

Function Properties  (4)

TemplateBox[{1, {1, /, 3}, x}, QBinomial] has both singularities and discontinuities for and for :

TemplateBox[{1, {1, /, 3}, x}, QBinomial] is neither non-negative nor non-positive:

QBinomial is neither convex nor concave:

TraditionalForm formatting:

Differentiation  (2)

The first derivative with respect to n when m=1/2:

The first derivative with respect to m when n=1 and q=2:

Higher derivatives with respect to m:

Plot the higher derivatives with respect to m when n=3 and q=2:

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

The Taylor expansion at a generic point:

Generalizations & Extensions  (1)

QBinomial can be applied to a power series:

Applications  (4)

Explicit combinatorial construction of QBinomial:

-binomial is a generating function for the sequence in a grid-shading problem:

Compare to explicit counting:

Elements in the -Pascal triangle satisfy two recurrence relations:

The number of subspaces in the -dimensional vector space over with prime-power :

Total number of subspaces in three-dimensional vector space over :

Check using recurrence equation for Galois numbers:

Properties & Relations  (2)

Use FunctionExpand and FullSimplify to manipulate expressions containing QBinomial:

Build series expansions:

Wolfram Research (2008), QBinomial, Wolfram Language function, https://reference.wolfram.com/language/ref/QBinomial.html.

Text

Wolfram Research (2008), QBinomial, Wolfram Language function, https://reference.wolfram.com/language/ref/QBinomial.html.

CMS

Wolfram Language. 2008. "QBinomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/QBinomial.html.

APA

Wolfram Language. (2008). QBinomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/QBinomial.html

BibTeX

@misc{reference.wolfram_2025_qbinomial, author="Wolfram Research", title="{QBinomial}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/QBinomial.html}", note=[Accessed: 07-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_qbinomial, organization={Wolfram Research}, title={QBinomial}, year={2008}, url={https://reference.wolfram.com/language/ref/QBinomial.html}, note=[Accessed: 07-June-2025 ]}