Quotient

Quotient[m,n]

gives the integer quotient of m and n.

Quotient[m,n,d]

uses an offset d.

Details

  • Quotient is also known as the ratio or fraction.
  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • Quotient[m,n] gives the greatest integer no larger than m/n.
  • Quotient[m,n,d] returns x such that d<=m-nx<d+n.

Examples

open allclose all

Basic Examples  (2)

Compute the quotient of two numbers:

Plot the sequence of quotients:

Scope  (16)

Numerical Evaluation  (8)

Quotient works over integers:

Rational numbers:

Inexact real numbers:

Exact numbers:

Complex numbers:

Compute for large integers:

Compute quotients with offsets:

Quotient threads elementwise over lists:

Symbolic Manipulation  (8)

Reduce inequalities:

Refine symbolic expressions:

Simplify expressions:

Expand Quotient in terms of Floor:

Express Quotient as a piecewise function:

Evaluate integrals:

Recurrence equation:

Generating function:

Applications  (11)

Basic Applications  (6)

Table of the quotients of the first 100 pairs of integers:

Plot the quotient of two integers:

Plot the quotient of a number of division by 2:

Plot the quotient:

Produce a 3D plot of the quotient of two functions:

Plot the quotient of two complex variables:

Number Theory  (5)

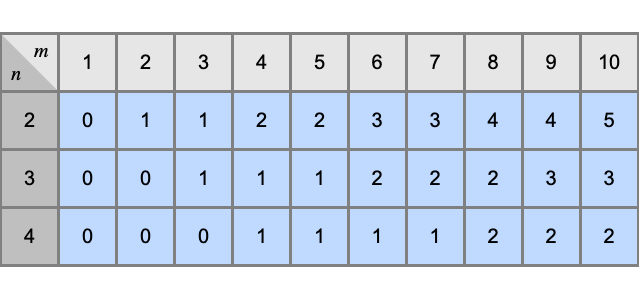
Use NestWhileList to compute Quotient for positive arguments:

Compare with the following:

Demonstrate how division works:

Count the number of positive integers less than 1000 divisible by 2 or 3, but not divisible by 6:

Direct count:

Implement the Euclidean algorithm:

Compare with:

Simplify expressions containing Quotient:

Properties & Relations  (6)

The first part of QuotientRemainder is the Quotient:

Quotient[m,n] is equivalent to Floor[m/n] for integers:

n*Quotient[m,n,d]+Mod[m,n,d] is always equal to m:

Quotient[m,n]+FractionalPart[m/n] is always equal to for positive integers:

Use PiecewiseExpand to express as a piecewise function:

Simplify expressions containing Quotient:

Possible Issues  (1)

Quotient does not automatically resolve the value:

Interactive Examples  (1)

Plot the quotient of two integers:

Neat Examples  (2)

Plot the arguments of the Fourier transform of the Quotient:

Plot the Ulam spiral of the Quotient:

Wolfram Research (1988), Quotient, Wolfram Language function, https://reference.wolfram.com/language/ref/Quotient.html (updated 2002).

Text

Wolfram Research (1988), Quotient, Wolfram Language function, https://reference.wolfram.com/language/ref/Quotient.html (updated 2002).

CMS

Wolfram Language. 1988. "Quotient." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Quotient.html.

APA

Wolfram Language. (1988). Quotient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Quotient.html

BibTeX

@misc{reference.wolfram_2024_quotient, author="Wolfram Research", title="{Quotient}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Quotient.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_quotient, organization={Wolfram Research}, title={Quotient}, year={2002}, url={https://reference.wolfram.com/language/ref/Quotient.html}, note=[Accessed: 22-November-2024 ]}