RFixedPoints

RFixedPoints[eqn,a[n],n]

gives the fixed points for a recurrence equation.

RFixedPoints[{eqn1,eqn2,…},{a1[n],a2[n],…},n]

gives the fixed points for a system of recurrence equations.

Details and Options

  • Fixed points are also known as equilibrium points or stationary points.
  • RFixedPoints is typically used to locate all fixed points for nonlinear discrete-time systems, such as frequently occur in ecological, economical or technical modeling. The local behavior at these fixed points can be analyzed using RStabilityConditions.
  • For a system of recurrence equations 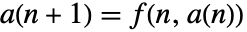, a point 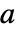is a fixed point iff 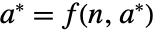. In effect, the initial value 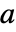remains stationary; if you initialize at 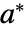you stay at .
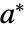  • RFixedPoints returns a list of the form {{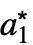,,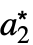…},…}, where {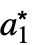,,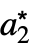…} is a fixed point.
  • RFixedPoints works for linear and nonlinear ordinary difference equations.
  • The following options can be given:
  • Assumptions$Assumptionsassumptions on parameters

Examples

open allclose all

Basic Examples  (6)

Find the fixed point for the recursion :

Find the fixed point for the recursion :

Find the fixed points for the recursion :

Check the stability of the point:

Plot several solutions for different values of a:

Find the fixed points of a two-dimensional system:

Determine the stability conditions:

Plot the parameter region for which the system is stable:

Find the fixed points of a nonlinear recurrence equation:

Determine the stability:

Use a cobweb plot to demonstrate the stability:

Consider a system , :

Calculate the differences and to generate the vector field plot of the system:

Scope  (14)

Linear Equations  (4)

Find the fixed point for the recursion :

A first-order linear inhomogeneous equation:

Determine the stability condition:

Plot the solution for :

Plot the solution for :

Second-order linear equation:

Determine the stability conditions:

Plot the stability region:

Third-order linear equation:

Determine the stability conditions:

Plot the stability region:

Nonlinear Equations  (3)

The fixed points of a logistic equation:

Analyze the stability of the points:

Plot the solution:

Use a cobweb plot to demonstrate the stability:

The fixed points of a Riccati equation:

Use a cobweb plot to demonstrate the stability:

Higher-order equations:

Linear Systems  (5)

The fixed points of a linear system of uncoupled equations:

Linear system with constant coefficients:

Use VectorPlot to visualize the fixed point:

Solve the system with boundary conditions:

Plot the solution:

A first-order system with periodic coefficients:

Compare to the general solution:

A first-order system with eventually periodic coefficients:

10x10 discrete linear system with random constant coefficients:

Nonlinear Systems  (2)

A nonlinear first-order system:

Determine the stability of the fixed points:

The fixed points and the stability of a linear fractional system:

Use VectorPlot to visualize the stability at point :

Applications  (8)

Numerical Analyses  (3)

Analyze the stability of the Newton–Raphson difference equation for the function x2-a:

Find fixed points:

Visualize the stability of the fixed points for :

Analyze the stability of the Newton–Raphson difference equation for the function x1/3:

The equation has one unstable fixed point at origin:

The instability of the point means that Newton's method cannot be used in this case:

Consider a system of linear equations , where:

Construct the Gauss–Seidel difference equation for the system:

Find the fixed point of the Gauss–Seidel equation:

Solve the system using LinearSolve:

Physics  (1)

Consider an object with temperature in the environment with constant temperature . Let be the change in temperature of the object over a time interval . Newton's law of cooling states that the rate of change of the temperature of an object is proportional to the difference of the temperature of the object and its surroundings:

Find the fixed points:

The fixed point is stable if :

Solution of the equation:

Simulate the cooling process:

Simulate the heating process:

Ecology and Biology  (2)

Stability analysis for a competing species model:

Solve the equation for given initial conditions and plot the solution:

Stability analysis for a predator-prey model:

Vector field plot of the model:

Use RecurrenceTable to solve the system numerically:

Economics  (2)

Consider a bank account with initial deposit , annual rate and monthly withdrawal amount . The amount in the savings account after months satisfies a recurrence equation:

The equation has unstable fixed point :

The amount in the account will increase each month if :

Stability analysis for the logistic equation:

Check the stability of the fixed points:

Check the stability for given range of the parameter :

Visualize the stability for :

Visualize the stability for :

Properties & Relations  (8)

RFixedPoints returns fixed points for recurrence equations:

Use RStabilityConditions to determine the stability for all fixed points of a recurrence equation:

Analyze the stability at specific fixed points:

Use RFixedPoints to find all fixed points of a nonlinear recurrence equation:

Use Solve to find the fixed points:

The fixed points for an n^(th)-order recurrence equation are n-dimensional vectors:

The fixed points for a system of n first-order recurrence equations are n-dimensional vectors:

Find the fixed points for a system of two ODEs:

Use RSolveValue to solve the system using fixed point as the initial condition:

Use RSolveValue to solve the system for given initial conditions:

Plot the solution:

Analyze the stability of a nonlinear ODE:

Solve the ODE using RecurrenceTable:

Plot the solution:

Analyze the stability of a recurrence equation with eventually constant coefficients:

Find a series solution using AsymptoticRSolveValue:

Plot the asymptotic solution:

Wolfram Research (2024), RFixedPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/RFixedPoints.html.

Text

Wolfram Research (2024), RFixedPoints, Wolfram Language function, https://reference.wolfram.com/language/ref/RFixedPoints.html.

CMS

Wolfram Language. 2024. "RFixedPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RFixedPoints.html.

APA

Wolfram Language. (2024). RFixedPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RFixedPoints.html

BibTeX

@misc{reference.wolfram_2024_rfixedpoints, author="Wolfram Research", title="{RFixedPoints}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RFixedPoints.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rfixedpoints, organization={Wolfram Research}, title={RFixedPoints}, year={2024}, url={https://reference.wolfram.com/language/ref/RFixedPoints.html}, note=[Accessed: 22-December-2024 ]}