RFixedPoints
RFixedPoints[eqn,a[n],n]
给出递归方程的不动点.
RFixedPoints[{eqn1,eqn2,…},{a1[n],a2[n],…},n]
给出递归方程组的不动点.
更多信息和选项

- 不动点也称为平衡点或驻点.
- RFixedPoints 通常用于定位非线性离散时间系统的所有不动点,在生态、经济或技术建模中经常出现. 这些不定点处的局部行为可以使用 RStabilityConditions 分析.
- 对于递归方程组
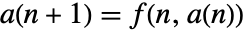 ,当且仅当
,当且仅当 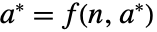 时,点
时,点 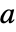 为不动点. 实际上,初始值
为不动点. 实际上,初始值 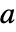 保持不变;如果在
保持不变;如果在 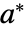 处初始化,则保持在
处初始化,则保持在 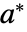 处.
处. - RFixedPoints 返回形如 {{
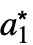 ,
,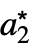 ,…},…} 的列表,其中 {
,…},…} 的列表,其中 {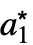 ,
,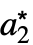 ,…} 是不动点.
,…} 是不动点. - RFixedPoints 适用于线性和非线性常微分方程.
- 可以提供以下选项:
-
Assumptions $Assumptions 关于参数的假设
范例
打开所有单元关闭所有单元基本范例 (6)
范围 (14)
应用 (8)
数值分析 (3)
物理学 (1)
生态学和生物学 (2)
属性和关系 (8)
RFixedPoints 返回递归方程的不动点:
使用 RStabilityConditions 确定递归方程所有不动点的稳定性:
使用 RFixedPoints 求非线性递归方程的所有不动点:
使用 Solve 求不动点:
使用 RSolveValue 求解以不动点为初始条件的系统:
使用 RSolveValue 求解给定初始条件下的系统:
使用 RecurrenceTable 求解常微分方程:
使用 AsymptoticRSolveValue 求级数解:
Wolfram Research (2024),RFixedPoints,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RFixedPoints.html.
文本
Wolfram Research (2024),RFixedPoints,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RFixedPoints.html.
CMS
Wolfram 语言. 2024. "RFixedPoints." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RFixedPoints.html.
APA
Wolfram 语言. (2024). RFixedPoints. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RFixedPoints.html 年