RStability
RStabilityConditions[eqn,a[n],n]
再帰方程式の固定点と安定性条件を与える.
RStabilityConditions[{eqn1,eqn2,…},{a1[n],a2[n],…},n]
再帰方程式系の固定点と安定性条件を与える.
RStabilityConditions[{eqn1,eqn2,…},{a1[n],a2[n],…},n,{pnt1,pnt2,…}]
指定された固定点についての安定性条件だけを与える.
詳細とオプション

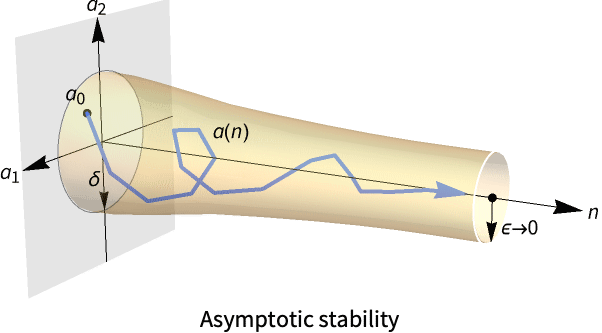
- 安定性は漸近安定性として,また,固定点は平衡点または停留点としても知られている.
- RStabilityConditionsは,固定点近くの長期的な挙動の定性的解析によく使われる.系が安定していれば,十分近いなら解は固定点に収束する.
- 再帰方程式
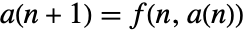 の系について,点
の系について,点 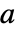 は
は 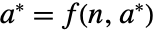 のときかつそのときに限って固定点である.実際,
のときかつそのときに限って固定点である.実際,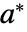 で初期化すると
で初期化すると 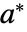 のままなので,
のままなので,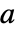 の初期値は固定点のままである.
の初期値は固定点のままである. 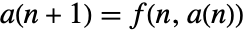 と
と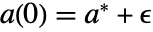 について,十分小さい
について,十分小さい 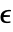 について
について![TemplateBox[{{a, (, n, )}, n, infty}, Limit2Arg]=a^* TemplateBox[{{a, (, n, )}, n, infty}, Limit2Arg]=a^*](Files/RStabilityConditions.ja/10.png) のときかつそのときに限って,固定点
のときかつそのときに限って,固定点 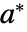 は漸近的に安定している.
は漸近的に安定している.- RStabilityConditionsは{{{
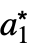 ,
,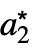 ,…},cond},…}の形のリストを返す.ただし,{
,…},cond},…}の形のリストを返す.ただし,{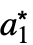 ,
,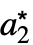 ,…}は固定点である.
,…}は固定点である. - RStabilityConditionsは固定点の局所的安定性のために十分な条件を与える.線形系については,これらの条件は大域的安定性の条件でもある.
- RStabilityConditionsは,線形と非線形の常差分方程式に使うことができる.
- 次は,使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定
例題
すべて開くすべて閉じる例 (8)
VectorPlotを使って安定性を可視化する:
スコープ (14)
オプション (1)
Assumptions (1)
Assumptionsがないと,安全性についてパラメータに条件が生まれる:
Assumptionsを使うと条件が簡約されることが多い:
アプリケーション (8)
数値解析 (3)
関数x2-aについてのニュートン・ラフソン(Newton–Raphson)差分方程式を解析する:
関数x1/3についてのニュートン・ラフソン差分方程式の安定性を解析する:
点の不安定性は,この場合はニュートン法が使えないことを意味する:
この系についてのガウス・サイデル(Gauss–Seidel)差分方程式を構築する:
LinearSolveを使って系を解く:
物理学 (1)
生態学と生物学 (2)
特性と関係 (8)
RStabilityConditionsは再帰方程式の固定点と安定性条件を返す:
RFixedPointsを使って再帰方程式のすべての固定点を求める:
RFixedPointsを使って非線形再帰方程式の固定点を求める:
Solveを使って固定点を求める:
RStabilityConditionsを使って非線形方程式の安定性を判定する:
n 個の一次再帰方程式の系の固定点は n 次元ベクトルである:
RSolveValueで,定常点を初期条件として使って系を解く:
RSolveValueを使って指定された初期条件について系を解く:
RecurrenceTableを使って常微分方程式を解く:
AsymptoticRSolveValueを使って級数解を求める:
考えられる問題 (2)
安定性についての条件が可能な限り最も単純なものではないことがある:
与えられた点が固定点ではないのでRStabilityConditionsはうまくいかない:
まずRFixedPoints 使って方程式のすべての固定点を求める:
テキスト
Wolfram Research (2024), RStability, Wolfram言語関数, https://reference.wolfram.com/language/ref/RStabilityConditions.html.
CMS
Wolfram Language. 2024. "RStability." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RStabilityConditions.html.
APA
Wolfram Language. (2024). RStability. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RStabilityConditions.html