RadialityCentrality
グラフ g 中の頂点の放射中心性のリストを与える.
RadialityCentrality[g,"In"]
有向グラフ g の入中心性のリストを与える.
RadialityCentrality[g,"Out"]
有向グラフ g の出中心性のリストを与える.
RadialityCentrality[{vw,…},…]
規則 vw を使ってグラフ g を指定する.
詳細

- 放射入中心性は統合中心性としても知られている.
- RadialityCentralityは,到達可能な近傍にある他のすべての頂点との距離が直径に比べて短い頂点に高い中心性を与える.
- 頂点
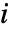 の放射出中心性は頂点
の放射出中心性は頂点 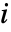 の出成分
の出成分 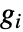 を使って計算され,
を使って計算され,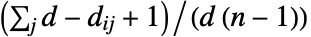 で与えられる.ただし,
で与えられる.ただし,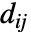 は
は 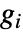 中の
中の 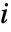 から
から 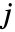 までの距離,
までの距離,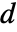 は
は 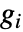 の直径であり,総和は
の直径であり,総和は 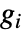 中の頂点について求められる.
中の頂点について求められる. - 頂点
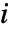 の放射入中心性は頂点
の放射入中心性は頂点 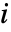 の入成分
の入成分 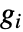 を使って計算され,
を使って計算され,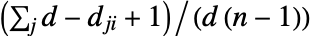 で与えられる.ただし,
で与えられる.ただし,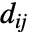 は
は 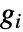 中の
中の 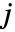 から
から 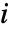 までの距離,
までの距離,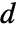 は
は 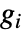 の直径であり,総和は
の直径であり,総和は 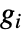 中の頂点について求められる.
中の頂点について求められる. - 孤立頂点の放射中心性は0であるとみなされる.
- RadialityCentralityは,無向グラフ,有向グラフ,重み付きグラフ,多重グラフ,混合グラフに使うことができる.
例題
すべて開くすべて閉じるスコープ (8)
RadialityCentralityは無向グラフに使うことができる:
RadialityCentralityは大きいグラフに使うことができる:
アプリケーション (2)
特性と関係 (3)
RadialityCentralityはGraphDistanceMatrixを使って計算することができる:
VertexIndexを使って特定の頂点の中心性を得る:
テキスト
Wolfram Research (2012), RadialityCentrality, Wolfram言語関数, https://reference.wolfram.com/language/ref/RadialityCentrality.html (2015年に更新).
CMS
Wolfram Language. 2012. "RadialityCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/RadialityCentrality.html.
APA
Wolfram Language. (2012). RadialityCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RadialityCentrality.html