

Rectangle
Details and Options

- Rectangle can be used as a geometric region and a graphics primitive.
- Rectangle represents the region
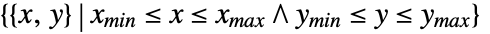 .
. - Rectangle[] is equivalent to Rectangle[{0,0}]. »
- Rectangle can be used in Graphics.
- In graphics, the points {xi,yi} can be Scaled, Offset, ImageScaled, and Dynamic expressions.
- The option RoundingRadius->r can be used to specify rounded corners rendered using circles of radius r.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm and color.
- CanonicalizePolygon can be used to convert a rectangle to an explicit Polygon object.

Examples
open all close allBasic Examples (5)
Scope (17)
Graphics (7)
Specification (3)
Styling (1)
Coordinates (3)
Regions (10)
Get conditions for point membership:
Integrate over a rectangle:
Applications (6)
The trajectory of the square wheel:
A Rectangle with equal side lengths is a square:
Maximize the area of a rectangle with a fixed perimeter:
Properties & Relations (9)
Use Rotate to get all possible rectangles:
Rectangle is a special case of Cuboid:
Rectangle is a special case of Parallelogram:
Rectangle is a special case of Polygon:
Rectangle is the union of two Triangle objects:
ImplicitRegion can represent any Rectangle region:
ParametricRegion can represent any Rectangle region:
MeshRegion can represent any Rectangle region:
BoundaryMeshRegion can represent any Rectangle region:
Possible Issues (1)
RoundingRadius only affects Graphics:
See Also
Polygon Parallelogram Cuboid Raster Inset GraphicsGrid Rotate BoundingRegion
Function Repository: Rhombus
Related Guides
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2014 (10.0) ▪ 2019 (12.0)
Text
Wolfram Research (1988), Rectangle, Wolfram Language function, https://reference.wolfram.com/language/ref/Rectangle.html (updated 2019).
CMS
Wolfram Language. 1988. "Rectangle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Rectangle.html.
APA
Wolfram Language. (1988). Rectangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rectangle.html
BibTeX
@misc{reference.wolfram_2025_rectangle, author="Wolfram Research", title="{Rectangle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Rectangle.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_rectangle, organization={Wolfram Research}, title={Rectangle}, year={2019}, url={https://reference.wolfram.com/language/ref/Rectangle.html}, note=[Accessed: 09-March-2026]}