Regularization

Regularization

is an option for Sum and Product that specifies what type of regularization to use.

Details

  • Regularization affects only results for divergent sums and products.
  • The following settings can be used to specify regularization procedures for sums of the form :
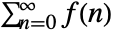  • "Abel"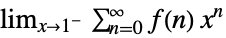
    "Borel"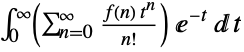
    "Cesaro"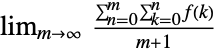
    "Dirichlet"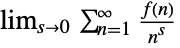
  • For alternating sums 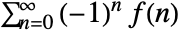, the setting "Euler" gives .
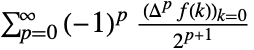  • The following setting can be used to specify a regularization procedure for products :
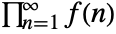  • "Dirichlet"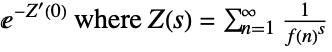
  • Regularization->None specifies that no regularization should be used.
  • For multiple sums and products, the same regularization is by default used for each variable.
  • Regularization->{reg1,reg2,…} specifies regularization regi for the i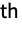^(th) variable.

Examples

open allclose all

Basic Examples  (3)

The following sum does not converge:

Using Abel regularization will produce a finite value:

In this case the Abel-regularized sum does not exist:

However, the stronger Borel regularization produces a finite value:

A regularized value of a divergent product:

Scope  (5)

Apply Abel regularization to sum a divergent polynomial-exponential series:

Use Borel regularization to sum a divergent hypergeometric series:

Apply Cesaro regularization to sum a divergent trigonometric series:

Sum a divergent logarithmic series using Dirichlet regularization:

Apply Euler regularization to sum a divergent geometric series:

Applications  (1)

The regularized sum of all the natural numbers is :

Wolfram Research (2008), Regularization, Wolfram Language function, https://reference.wolfram.com/language/ref/Regularization.html.

Text

Wolfram Research (2008), Regularization, Wolfram Language function, https://reference.wolfram.com/language/ref/Regularization.html.

CMS

Wolfram Language. 2008. "Regularization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Regularization.html.

APA

Wolfram Language. (2008). Regularization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Regularization.html

BibTeX

@misc{reference.wolfram_2025_regularization, author="Wolfram Research", title="{Regularization}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Regularization.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_regularization, organization={Wolfram Research}, title={Regularization}, year={2008}, url={https://reference.wolfram.com/language/ref/Regularization.html}, note=[Accessed: 18-April-2025 ]}