Regularization

Regularization

SumおよびProductのオプションで，どのタイプの正規化を使うかを指定する．

詳細

  • 正規化は発散する総和と積の結果にのみ影響する．
  • 次の設定を使って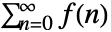の形の総和の正規化手続きを指定することができる．
  • "Abel"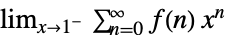
    "Borel"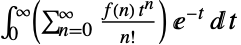
    "Cesaro"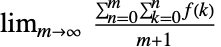
    "Dirichlet"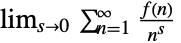
  • 交代和 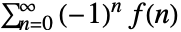の場合，設定を"Euler"にすると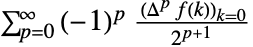が返される．
  • 次の設定を使って積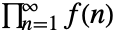の正規化手続きを指定することができる．
  • "Dirichlet"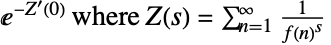
  • Regularization->Noneは正規化を行わないように指定する．
  • 多重和と多重積については，デフォルトで各変数に使われるのと同じ正規化が使われる．
  • Regularization->{reg1,reg2,…}は i 番目の変数に対する正規化 regiを指定する．

例題

すべて開くすべて閉じる

例  (3)

次の総和は収束しない：

アーベル(Abel)の正規化を使うと有限値が生成される：

次の場合は，アーベルの正規化による総和は存在しない：

しかし，より強力なボレル(Borel)の正規化を使うと有限値が得られる：

発散する積の正規化された値：

スコープ  (5)

アーベルの正規化を適用して，発散する多項式指数級数の総和を求める：

ボレルの正規化を用いて，発散する超幾何級数の総和を求める：

チェザーロの正規化を適用して，発散する三角級数の総和を得る：

ディリクレの正規化を用いて，発散する対数級数の総和を得る：

オイラーの正規化を適用して，発散する幾何級数の総和を得る：

アプリケーション  (1)

全自然数の正規化された総和はである：

Wolfram Research (2008), Regularization, Wolfram言語関数， https://reference.wolfram.com/language/ref/Regularization.html.

テキスト

Wolfram Research (2008), Regularization, Wolfram言語関数， https://reference.wolfram.com/language/ref/Regularization.html.

CMS

Wolfram Language. 2008. "Regularization." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Regularization.html.

APA

Wolfram Language. (2008). Regularization. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Regularization.html

BibTeX

@misc{reference.wolfram_2024_regularization, author="Wolfram Research", title="{Regularization}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Regularization.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regularization, organization={Wolfram Research}, title={Regularization}, year={2008}, url={https://reference.wolfram.com/language/ref/Regularization.html}, note=[Accessed: 22-November-2024 ]}