Regularization

Regularization

是 Sum 和 Product 的一个选项，指定所使用的正规化类型.

更多信息

  • 正规化仅影响求和发散和求乘积发散的结果.
  • 下列设置可以用于指定形如 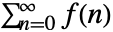的求和的正规化过程：
  • "Abel"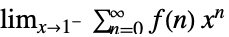
    "Borel"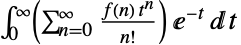
    "Cesaro"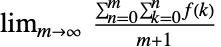
    "Dirichlet"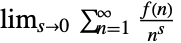
  • 对于交替和 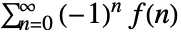，设置 "Euler" 给出 .
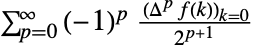  • 下列设置可以用来对乘积 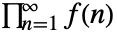指定一个正规化过程：
  • "Dirichlet"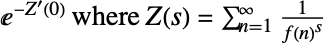
  • Regularization->None 表示不使用正规化.
  • 对于多重求和以及多重求乘积，默认情况下对每个变量使用相同的正规化.
  • Regularization->{reg1,reg2,…} 指定对第 i 个变量用正规化 regi.

范例

打开所有单元关闭所有单元

基本范例  (3)

下面的求和不收敛：

用 Abel 正规化将产生一个有限值：

在这种情况下，Abel 正规化的求和并不存在：

然而，更强的 Borel 正规化将产生一个有限值：

一个发散乘求积的正规化值：

范围  (5)

应用阿贝尔正规化方法以对发散多项式指数级数求和：

使用 Borel 正规化以对发散超几何级数求和：

应用 Cesaro 正规化以对发散三角级数求和：

使用 Dirichlet 正规化以对发散对数级数求和：

应用欧拉正规化以对发散几何级数求和：

应用  (1)

所有自然数的正规化和是 :

Wolfram Research (2008)，Regularization，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Regularization.html.

文本

Wolfram Research (2008)，Regularization，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Regularization.html.

CMS

Wolfram 语言. 2008. "Regularization." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Regularization.html.

APA

Wolfram 语言. (2008). Regularization. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Regularization.html 年

BibTeX

@misc{reference.wolfram_2025_regularization, author="Wolfram Research", title="{Regularization}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Regularization.html}", note=[Accessed: 03-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_regularization, organization={Wolfram Research}, title={Regularization}, year={2008}, url={https://reference.wolfram.com/language/ref/Regularization.html}, note=[Accessed: 03-April-2025 ]}