RiemannSiegelTheta

RiemannSiegelTheta[t]

リーマン・ジーゲル(Riemann–Siegel)関数 TemplateBox[{t}, RiemannSiegelTheta]を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 実数 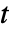について，TemplateBox[{t}, RiemannSiegelTheta]=Im(TemplateBox[{{{1, /, 4}, +, {{(, {ⅈ, , t}, )}, /, 2}}}, LogGamma])-t/2log pi が成立する．
  • TemplateBox[{t}, RiemannSiegelTheta]は臨界線上のリーマンのゼータ関数の研究から生じた．これは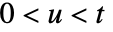，での TemplateBox[{{{1, /, 2}, +, {ⅈ, , u}}}, Zeta]のゼロの数と密接に関係している．
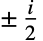  • TemplateBox[{t}, RiemannSiegelTheta]は，虚軸上のから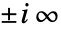の分枝切断線を除いて 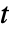の解析的な関数となる．
  • 特別な引数の場合，RiemannSiegelThetaは，自動的に厳密値を計算する．
  • RiemannSiegelThetaは任意の数値精度で評価できる．
  • RiemannSiegelThetaは自動的にリストに縫い込まれる．
  • RiemannSiegelThetaは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (6)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける級数展開：

特異点における級数展開：

スコープ  (28)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のRiemannSiegelTheta関数を計算することもできる：

特定の値  (2)

ゼロにおける値：

RiemannSiegelTheta[x]の正の最小値を求める：

可視化  (2)

RiemannSiegelThetaをプロットする：

RiemannSiegelTheta関数の実部をプロットする：

RiemannSiegelTheta関数の虚部をプロットする：

関数の特性  (11)

RiemannSiegelThetaはすべての実数値について定義される：

複素領域：

RiemannSiegelThetaの関数範囲：

RiemannSiegelThetaは要素単位でリストに縫い込まれる：

RiemannSiegelThetaは x の解析関数である：

RiemannSiegelThetaは特定の範囲で非増加である：

RiemannSiegelThetaは単射ではない：

RiemannSiegelThetaは全射である：

RiemannSiegelThetaは非負でも非正でもない：

RiemannSiegelThetaは特異点も不連続点も持たない：

RiemannSiegelThetaは凸でも凹でもない：

TraditionalFormによる表示：

微分  (3)

についての一次導関数：

についての高次導関数：

についての高次導関数をプロットする：

についての 次導関数の式：

級数展開  (4)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

Infinityにおけるテイラー展開を求める：

任意の記号方向 について級数展開を求める：

生成点におけるテイラー展開：

一般化と拡張  (2)

原点における級数展開：

分岐点における級数展開：

アプリケーション  (3)

複素平面上で実部と虚部をプロットする：

Sin[RiemannSiegelTheta[t]]とRiemannSiegelZ[t]の根の交差示す：

Gram pointを計算する：

RiemannSiegelZが連続する点について符号を変えるよいGram点を表示する：

悪いGram点を示す：

特性と関係  (3)

RiemannSiegelThetaはLogGammaに関連している：

RiemannSiegelZはRiemannSiegelThetaとZetaによって表すことができる：

超越方程式の根を数値的に求める：

考えられる問題  (2)

$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

機械数の入力で高精度の結果が得られることがある：

おもしろい例題  (1)

RiemannSiegelThetaのリーマン(Riemann)面：

Wolfram Research (1991), RiemannSiegelTheta, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html （2023年に更新）.

テキスト

Wolfram Research (1991), RiemannSiegelTheta, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html （2023年に更新）.

CMS

Wolfram Language. 1991. "RiemannSiegelTheta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html.

APA

Wolfram Language. (1991). RiemannSiegelTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html

BibTeX

@misc{reference.wolfram_2024_riemannsiegeltheta, author="Wolfram Research", title="{RiemannSiegelTheta}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riemannsiegeltheta, organization={Wolfram Research}, title={RiemannSiegelTheta}, year={2023}, url={https://reference.wolfram.com/language/ref/RiemannSiegelTheta.html}, note=[Accessed: 05-November-2024 ]}